题目列表(包括答案和解析)
如图，正四棱锥S－ABCD的底面边长为a，侧棱长为2a，点P、Q分别在BD和SC上，并且BP∶PD＝1∶2，PQ∥平面SAD，求线段PQ的长．
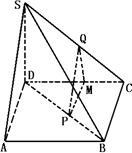
如图，正四棱锥S－ABCD的底面是边长为a正方形，O为底面对角线交点，侧棱长是底面边长的
倍，P为侧棱SD上的点．
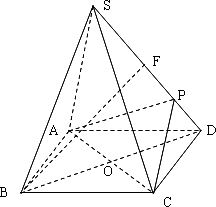
(Ⅰ)求证：AC⊥SD；
(Ⅱ)若SD⊥平面PAC，F为SD中点，求证：BF∥平面PAC；
(Ⅲ)在(Ⅱ)的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC．若存在，求SE：EC的值；若不存在，试说明理由．
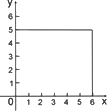
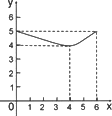
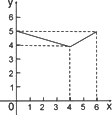
如图正四棱锥S－ABCD的底面边长为4
，高SE＝8，点F在高SE上，且SF＝x，记过点A，B，C，D，F的球的半径为R(x)，则函数R(x)的大致图像是
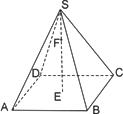
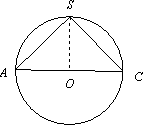
正四棱锥S－ABCD的5个顶点都在球O的表面上，过球心O的一个截面如图，棱锥的底面边长为1，则球O的表面积为________；
一个四棱锥S－ABCD的底面是边长为a的正方形，侧面展开图如图(1)所示．
(1)请画出四棱锥S－ABCD的示意图，问是否存在一条
侧棱与底面垂直？若存在，请给出证明；
(2)若SC为四棱锥中最长的侧棱，点E为AB的中点．
①求二面角E－SC－D的大小；
②求点D到平面SEC的距离．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com