
题目列表(包括答案和解析)
(本题满分12分)有混在一起质地均匀且粗细相同的长分别为1![]() 、2
、2![]() 、3
、3![]() 的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.
的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.
(1)若用ξ表示新焊成的钢管的长度(焊接误差不计),试求随机变量![]() 的分布列及
的分布列及![]() ;
;
(2)设![]() 的取值从小到大依次为
的取值从小到大依次为![]() 数列
数列![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列,设
的等差数列,设![]() ,当
,当![]() 时,求
时,求![]() 的值。
的值。
 、2
、2 、3
、3 的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根.
的钢管各3根(每根钢管附有不同的编号),现随意抽取4根(假设各钢管被抽取的可能性是均等的),再将抽取的4根首尾相接焊成笔直的一根. 的分布列及
的分布列及 ;
; 的取值从小到大依次为
的取值从小到大依次为 数列
数列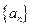 是首项为1,公差为
是首项为1,公差为 的等差数列,设
的等差数列,设 ,当
,当 时,求
时,求 的值。
的值。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com