
题目列表(包括答案和解析)
(1)分别写出x∈[0,1)时y=f(x)的解析式f1(x)和x∈[1,2)时y=f(x)的解析式f2(x);并猜想x∈[n,n+1],n≥-1,n∈Z时y=f(x)的解析式f n+1(x)(用x和n表示)(不必证明);
(2)当x=n+![]() (n≥-1,n∈Z)时,y=f n+1(x)x∈[n,n+1),(n≥-1,n∈Z)的图象上有点列A n+1(x,f(x))和点列B n+1(n+1,f(n+1)),线段A n+1B n+2与线段B n+1A n+2的交点C n+1,求点C n+1的坐标(a n+1(x),b n+1(x));
(n≥-1,n∈Z)时,y=f n+1(x)x∈[n,n+1),(n≥-1,n∈Z)的图象上有点列A n+1(x,f(x))和点列B n+1(n+1,f(n+1)),线段A n+1B n+2与线段B n+1A n+2的交点C n+1,求点C n+1的坐标(a n+1(x),b n+1(x));
(3)在前面(1)(2)的基础上,请你提出一个点列C n+1(a n+1(x),b n+1(x))的问题,并进行研究,并写下你研究的过程.
(Ⅰ)分别写出x∈[0,1)时y=f(x)的解析式f1(x)和x∈[1,2)时y=f(x)的解析式f2(x);并猜想x∈[n,n+1),n≥-1,n∈Z时y=f(x)的解析式fn+1(x)(用x和n表示,不必证明);
(Ⅱ)当x=n+![]() (n≥-1,n∈Z)时,y=fn+1(x),x∈[n,n+1),(n≥-1,n∈Z)的图象上有点列An+1(x,f(x))和点列Bn+1(n+1,f(n+1)),线段An+1Bn+2与线段Bn+1An+2的交点Cn+1,求点Cn+1的坐标(an+1(x),bn+1(x));
(n≥-1,n∈Z)时,y=fn+1(x),x∈[n,n+1),(n≥-1,n∈Z)的图象上有点列An+1(x,f(x))和点列Bn+1(n+1,f(n+1)),线段An+1Bn+2与线段Bn+1An+2的交点Cn+1,求点Cn+1的坐标(an+1(x),bn+1(x));
(Ⅲ)在前面(Ⅰ)(Ⅱ)的基础上,请你提出一个点列Cn+1(an+1(x),bn+1(x))的问题,并进行研究,并写下你研究的过程.
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| 1 |
| 3 |
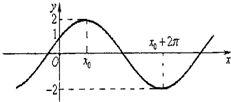
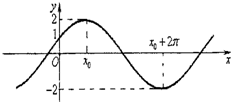
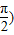 的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x,2)和(x+2π,-2).
的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x,2)和(x+2π,-2).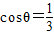 ,求f(2θ)的值.
,求f(2θ)的值.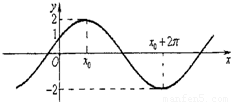
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<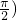 的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).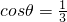 ,求f(2θ)的值.
,求f(2θ)的值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com