
题目列表(包括答案和解析)
按右下图所表示的算法,若输入的 是一个小于50的数,则输出的是( )
是一个小于50的数,则输出的是( )
A.2005 B.65 C.64 D.63

按下图所表示的算法,若输入的n是一个小于50的数,则输出的是
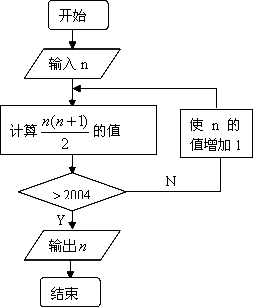
2005
65
64
63
(本小题满分13分)
为了适应新课改的要求,某重点高中在高一![]() 名新生中开设选修课。其中某老师开设的《趣味数学》选修课,在选课时设第
名新生中开设选修课。其中某老师开设的《趣味数学》选修课,在选课时设第![]() 次选修人数为
次选修人数为![]() 个,且第
个,且第![]() (
(![]() )次选课时,选《趣味数学》的同学人数比第
)次选课时,选《趣味数学》的同学人数比第![]() 次选修人数的一半还多
次选修人数的一半还多![]() 人。
人。
(Ⅰ)当![]() 时,写出数列
时,写出数列![]() 的一个递推公式,并证明数列
的一个递推公式,并证明数列![]() 是一个等比数列;
是一个等比数列;
(Ⅱ)求出用![]() 和
和![]() 表示的数列
表示的数列![]() 的通项公式。如果选《趣味数学》的学生越来越多,求
的通项公式。如果选《趣味数学》的学生越来越多,求![]() 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com