如图，在三棱柱中，侧面，为棱上异于的一点，，已知，求：

（Ⅰ）异面直线与的距离；

（Ⅱ）二面角的平面角的正切值.

【解析】第一问中，利用建立空间直角坐标系

解：（I）以B为原点，、分别为Y,Z轴建立空间直角坐标系.由于，

在三棱柱中有

,

设

又侧面，故. 因此是异面直线的公垂线，则，故异面直线的距离为1.

（II）由已知有故二面角的平面角的大小为向量与的夹角.

（本小题满分12分）已知f (x)＝(1＋x)^m＋(1＋2x)ⁿ(m，n∈N^*)的展开式中x的系数为11.
(1)求x²的系数的最小值；
(2)当x²的系数取得最小值时，求f (x)展开式中x的奇次幂项的系数之和．
解： (1)由已知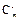＋2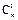＝11，∴m＋2n＝11，x²的系数为
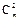＋2²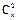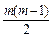＝＋2n(n－1)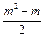＝＋(11－m)(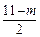－1)＝(m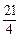－)²＋.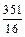
∵m∈N^*，∴m＝5时，x²的系数取最小值22，此时n＝3.
(2)由(1)知，当x²的系数取得最小值时，m＝5，n＝3，
∴f (x)＝(1＋x)⁵＋(1＋2x)³.设这时f (x)的展开式为f (x)＝a₀＋a₁x＋a₂x²＋^…＋a₅x⁵，
令x＝1，a₀＋a₁＋a₂＋a₃＋a₄＋a₅＝2⁵＋3³，
令x＝－1，a₀－a₁＋a₂－a₃＋a₄－a₅＝－1，
两式相减得2(a₁＋a₃＋a₅)＝60， 故展开式中x的奇次幂项的系数之和为30.

仔细阅读下面问题的解法：
设A=[0，1]，若不等式2^1-x-a＞0在A上有解，求实数a的取值范围．
解：由已知可得　a＜2^1-x
令f（x）=2^1-x，不等式a＜2^1-x在A上有解，
∴a＜f（x）在A上的最大值
又f（x）在[0，1]上单调递减，f（x）_max=f（0）=2
∴a＜2即为所求．
学习以上问题的解法，解决下面的问题：
（1）已知函数f（x）=x²+2x+3 （-2≤x≤-1）求f（x）的反函数及反函数的定义域A；
（2）对于（1）中的A，设g（x）=x∈A，试判断g（x）的单调性；（不证）
（3）又若B={x|＞2^x+a-5}，若A∩B≠Φ，求实数a的取值范围．