练习册

  • 练习册
  • 试题
    选修2-2第59页例1.例2 计算下列定积分: 变式1:计算:, (1),(2) 解:.(1) (2)利用导数的几何意义:与x=0,x=2所围图形是以(0,0)为圆心.2为半径的四分之一个圆.其面积即为 变式2: 求将抛物线和直线围成的图形绕轴旋转一周得到的几何体的体积. 分析:利用定积分的定义解题.应当画出草图. 解:先求出抛物线和直线交点坐标 利用定积分的定义易得: 变式3:在曲线上某一点A处作一切线使之与曲线以及轴所围的面积为.试求:在切点A的切线方程. 【查看更多】

     

    题目列表(包括答案和解析)

    为配合新课程的实施，乌鲁木齐市第一中学联合兄弟学校举行了“应用与创新”知识竞赛，共有1500名学生参加了这次竞赛（满分100分，得分全为整数）．为了解本次竞赛成绩情况，从中随机抽取了部分学生的竞赛成绩，进行统计，整理见下表：

     

    组别

    分     组

    频  数

    频率

    1

    49．5～59．5

    60

    0．12

    2

    59．5～69．5

    120

    0．24

    3

    69．5～79．5

    180

    0．36

    4

    79．5～89．5

    130

    5

    89．5～99．5

    0．02

    合      计

    1．00

    解答下列问题：

    （1）在这个问题中，总体是               ，样本是               ，

    样本容量＝                 ；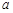

    （2）第四小组的频率＝                   ；

    （3）被抽取的学生成绩的中位数落在第几小组内？

    （4）若成绩在90分以上（含90分）的学生获一等奖，请你估计此次竞赛获一等奖的人数．

     

    查看答案和解析>>

    (选修1－2(A版)第37页A组第6题)在等差数列{an}中，若a10＝0，则有a1＋a2＋…＋an＝a1＋a2＋…＋a19－n(n＜19，n∈N+)成立．类比上述性质，在等比数列{bn}中，若b9＝1，则存在怎样的等式？

    查看答案和解析>>

    [选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．
    A．（选修4-1：几何证明选讲）
    如图，圆O的直径AB=8，C为圆周上一点，BC=4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，求线段AE的长．
    B．（选修4-2：矩阵与变换）
    已知二阶矩阵A有特征值λ1=3及其对应的一个特征向量α1=
    1
    1
    ，特征值λ2=-1及其对应的一个特征向量α2=
    1
    -1
    ，求矩阵A的逆矩阵A-1．
    C．（选修4-4：坐标系与参数方程）
    以平面直角坐标系的原点O为极点，x轴的正半轴为极轴，建立极坐标系（两种坐标系中取相同的单位长度），已知点A的直角坐标为（-2，6），点B的极坐标为(4，
    π
    2
    )    ，直线l过点A且倾斜角为
    π
    4
    ，圆C以点B为圆心，4为半径，试求直线l的参数方程和圆C的极坐标方程．
    D．（选修4-5：不等式选讲）
    设a，b，c，d都是正数，且x=
    		a2+b2
    ，y=
    		c2+d2
    ．求证：xy≥
    		(ac+bd)(ad+bc)
    ．

    查看答案和解析>>

    （教材江苏版第62页习题7）（1）已知数列an的通项公式为an=
    1
    n(n+1)
    ，则前n项的和
     
    ；（2）已知数列an的通项公式为an=
    1
    		n
    +
    		n+1
    ，则前n项的和
     
    ．

    查看答案和解析>>

    一等比数列{an}的首项a1=2-5，前11项的几何平均数为25，现从这11项中抽去一项，下余的十项的几何平均数为24，则抽去的一定是（　　）

    查看答案和解析>>


    同步练习册答案