练习册

  • 练习册
  • 试题
    3．确定集合的“包含关系 与求集合的“交.并.补 是学习集合的中心内容.解决问题时应根据问题所涉及的具体的数学内容来寻求方法. ① 区别∈与.与.a与{a}.φ与{φ}.{(1,2)}与{1,2}, ② AB时.A有两种情况:A＝φ与A≠φ. ③若集合A中有n个元素.则集合A的所有不同的子集个数为.所有真子集的个数是-1, 所有非空真子集的个数是. ④区分集合中元素的形式: 如, , , , , , . ⑤空集是指不含任何元素的集合..和的区别,0与三者间的关系.空集是任何集合的子集.是任何非空集合的真子集.条件为.在讨论的时候不要遗忘了的情况. ⑥符号“ 是表示元素与集合之间关系的.立体几何中的体现点与直线(面)的关系 ,符号“ 是表示集合与集合之间关系的.立体几何中的体现面与直线(面)的关系. 逻辑是研究思维形式及其规律的一门学科.是人们认识和研究问题不可缺少的工具.是为了培养学生的推理技能.发展学生的思维能力. 【查看更多】

     

    题目列表(包括答案和解析)

    举例说明集合间的包含关系与相等关系，并用图形直观表示．

    查看答案和解析>>

    集合P＝{α｜α＝n·90°＋45°，n∈Z}与集合Q＝{β｜β＝k·45°＋90°，k∈Z}之间的包含关系是________．

    查看答案和解析>>

    集合A={正方体}，B={直四棱柱}，C={正四棱柱}，D={长方体}，它们之间的包含关系是
     
    ．

    查看答案和解析>>

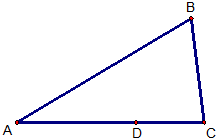    如图，已知△ABC，BC=9cm，现有两个质点甲、乙同时从C点出发，甲沿路线C→B→A以每秒2cm的速度匀速向前移动，乙沿路线C→A以每秒1cm的速度匀速向前移动，当甲到达B点时，乙到达D点，并满足
    CD
    CA
    =
    3
    8
    ，最后它们同时到达A点．
    （1）试判断△ABC的形状；
    （2）设在t时刻，甲、乙分别到达E、F处，试确定△CEF的面积S与t的关系，并求出S的最大值．

    查看答案和解析>>

    若A、B、C为三个集合，A∪B=B∩C，则集合A、C之间的包含关系是
    A⊆C
    A⊆C
    ．

    查看答案和解析>>


    同步练习册答案