一个机器人每一秒钟前进或后退一步，程序设计师让机器人先前进3步再后退2步的规律移动，如果将机器人放在数轴的原点，面向正的方向以一步的距离为一个单位长度．令P(n)表示第n s时机器人所在位置的坐标，且记P(0)＝0，则下列结论中错误的是(　　)

A．P(3)＝3                              B．P(5)＝1

C．P(2 003)>P(2 005)                    D．P(2 007)>P(2 008)

如图，面积为S的平面凸四边形的第i条边的边长记为a_i(i＝1,2,3,4)，此四边形内任一点P到第i条边的距离为h_i(i＝1,2,3,4)，若＝＝＝k，则(ih_i)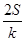＝.类比以上性质，体积为V的三棱锥的第i个面的面积记为S_i(i＝1,2,3,4)，此三棱锥内任一点Q到第i个面的距离记为h_i(i＝1,2,3,4)，若＝＝＝K，则(ih_i)＝(　　)

A.            B.              C.          D.

 

 

 

如下图所示，面积为S的平面凸四边形的第i条边的边长记为a_i，此四边形内任一点P到第i条边的距离记为h_i，若＝＝＝＝k，则＝.类比以上性质，体积为V的三棱锥的第i个面的面积记为S_i， 此三棱锥内任一点Q到第i个面的距离记为H_i，若＝＝＝＝k，则＝(　　)

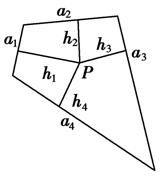
A.　　　　B.   C. 　　　　D.

 

等边△PQR中，P(0,0)、Q(4,0)，且R在第四象限内，则PR和QR所在直线的方程分别为(　　)

A．y＝±x

B．y＝±(x－4)

C．y＝x和y＝－(x－4)

D．y＝－x和y＝(x－4)

1.如果一个数列从第　　　　　　项起，每一项与前一项的　　　　　等于同一个常数，那么这个数列就叫做等比数列.这个常数叫做等比数列的　　　　　　　　　，通常用字母　　　　　表示.

2.如果a、G、b成等比数列，那么G叫做a与b的　　　，且G＝　　　　　(ab＞0).

3.等比数列的通项公式为a_n=　　　　　.

4.等比数列的前n项和公式为S_n=

5.对于正整数m,n,p,q,若m+n=p+q,则等比数列中a_m,a_n,a_p,a_q的关系为　　　　　.

6.若S_n为等比数列的前n项和，则S_k,S_2k-S _k,S_3k-S_2k,…,S_(m+1)k-S_mk,…成　　　　数列(k＞1且k∈N^*).