
题目列表(包括答案和解析)
已知下列结论:
①已知 为实数,则“
为实数,则“ ”是“
”是“ 成等比数列”的充要条件;
成等比数列”的充要条件;
②满足条件 的△ABC的个数为2;
的△ABC的个数为2;
③若两向量 的夹角为钝角,则实数
的夹角为钝角,则实数 的取值范围
的取值范围
为 ;
;
④若 为三角形中的最小内角,则函数
为三角形中的最小内角,则函数 的值域是
的值域是 ;
;
⑤某厂去年12月份产值是同年一月份产值的m倍,则该厂去年的月平均增长率
为 ;
;
则其中正确结论的序号是__________;
A.45° B.30° C.60° D.90°
已知a=(![]() ),b=(
),b=(![]() ),则( )
),则( )
A. a⊥b B. a∥b C.(a+b)⊥(a-b)
D. a与b的夹角为![]() .
.
已知两个单位向量 与
与 的夹角为
的夹角为 ,
若
,
若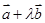 与
与 互相垂直,则
互相垂直,则 为( )
为( )
A. 或
或 B.
B. 或
或
C. 或
或 D.
D. 为任意实数
为任意实数
(文)已知向量 与
与 的夹角为
的夹角为 ,
, 则
则 等于( )
等于( )
A.5 B.4 C.3 D.1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com