
题目列表(包括答案和解析)
平面直角坐标系内的向量都可以用一有序实数对唯一表示,这使我们想到可以用向量作为解析几何的研究工具.如图,设直线
l的倾斜角为α(α≠90°).在l上任取两个不同的点 ,
, ,不妨设向量
,不妨设向量 的方向是向上的,那么向量
的方向是向上的,那么向量 的坐标是(
的坐标是( ).过原点作向量
).过原点作向量 ,则点P的坐标是(
,则点P的坐标是( ),而且直线OP的倾斜角也是α.根据正切函数的定义得
),而且直线OP的倾斜角也是α.根据正切函数的定义得
 ,
,
这就是《数学
2》中已经得到的斜率公式.上述推导过程比《数学2》中的推导简捷.你能用向量作为工具讨论一下直线的有关问题吗?例如:(1)
过点 ,平行于向量
,平行于向量 的直线方程;
的直线方程;
(2)
向量(A,B)与直线 的关系;
的关系;
(3)
设直线 和
和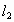 的方程分别是
的方程分别是
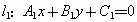

那么,
 ∥
∥ ,
, 的条件各是什么?如果它们相交,如何得到它们的夹角公式?
的条件各是什么?如果它们相交,如何得到它们的夹角公式?
(4)
点 到直线
到直线 的距离公式如何推导?
的距离公式如何推导?

某校九年级学生共300人,为了解这个年级学生的体能,从中随机抽取部分学生进行1分钟的跳绳测试,并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理,下面是这四名同学提供的部分信息:
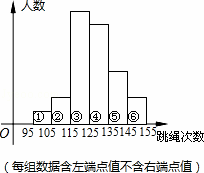
甲:将全体测试数据分成6组绘成直方图(如图);
乙:跳绳次数不少于105次的同学占96%;
丙:第①、②两组频率之和为0.12,且第②组与第⑥组频数都是4;
丁:第③组的频数比第④组的频数多2,且第③、④组的频数之和是第⑤组频数的4倍.
根据这四名同学提供的材料,请解答如下问题:
(1)这次跳绳测试共抽取多少名学生?第①、③组各有多少人?
(2)如果跳绳次数不少于135次为优秀,根据这次抽查的结果,估计全年级达到跳绳优秀的人数为多少?
(3)若分别以100、110、120、130、140、150作为第①、②、③、④、⑤、⑥组跳绳次数的代表,估计这批学生1分钟跳绳次数的平均值是多少?
(本小题满分14分)
为了调查老年人的身体状况,某老年活动中心对80位男性老年人和100位女性老年人在一次慢跑后的心率水平作了记录,记录结果如下列两个表格所示,
表1:80位男性老年人的心率水平的频数分布表(单位:次/分钟)
| 心率水平 |  | 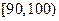 | 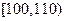 | 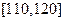 |
| 频数 | 10 | 40 | 20 | 10 |
| 心率水平 |  | 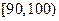 | 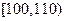 | 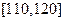 |
| 频数 | 10 | 20 | 50 | 20 |
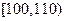 内的概率;
内的概率;
| 心率水平 性别 | 心率小于100 | 心率大于或等于100 | 合计 |
| 男性 |  | 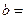 | |
| 女性 | 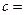 | 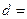 | |
| 合计 | | | 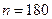 |
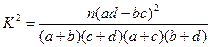
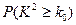 | 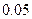 | 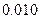 | 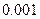 |
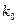 | 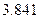 | 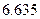 | 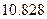 |
| 心率水平 |  |  |  |  |
| 频数 | 10 | 40 | 20 | 10 |
| 心率水平 |  |  |  |  |
| 频数 | 10 | 20 | 50 | 20 |
 内的概率;
内的概率;

| 心率水平 性别 | 心率小于100 | 心率大于或等于100 | 合计 |
| 男性 |  |  | |
| 女性 |  |  | |
| 合计 | | |  |

 |  |  |  |
 |  |  |  |
如图,直线 与抛物线
与抛物线 (常数
(常数 )相交于不同的两点
)相交于不同的两点 、
、 ,且
,且 (
( 为定值),线段
为定值),线段 的中点为
的中点为 ,与直线
,与直线 平行的切线的切点为
平行的切线的切点为 (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(1)用 、
、 表示出
表示出 点、
点、 点的坐标,并证明
点的坐标,并证明 垂直于
垂直于 轴;
轴;
(2)求 的面积,证明
的面积,证明 的面积与
的面积与 、
、 无关,只与
无关,只与 有关;
有关;
(3)小张所在的兴趣小组完成上面两个小题后,小张连 、
、 ,再作与
,再作与 、
、 平行的切线,切点分别为
平行的切线,切点分别为 、
、 ,小张马上写出了
,小张马上写出了 、
、 的面积,由此小张求出了直线
的面积,由此小张求出了直线 与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com