
题目列表(包括答案和解析)
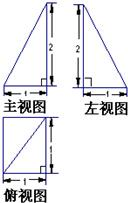 (理)设6张卡片上分别写有函数f1(x)=x、f2(x)=x2、f3(x)=x3、f4(x)=sinx、f5(x)=cosx和f6(x)=lg(|x|+1).
(理)设6张卡片上分别写有函数f1(x)=x、f2(x)=x2、f3(x)=x3、f4(x)=sinx、f5(x)=cosx和f6(x)=lg(|x|+1).下列说法中正确的是( )
A.“ ”是“
”是“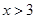 ”必要条件
”必要条件
B.命题“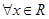 ,
, ”的否定是“
”的否定是“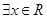 ,
,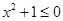 ”
”
C.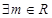 ,使函数
,使函数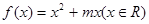 是奇函数
是奇函数
D.设 ,
, 是简单命题,若
是简单命题,若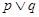 是真命题,则
是真命题,则 也是真命题
也是真命题
 是奇函数,(a,b,c都是整数),且f(1)=2,f(2)<3,f(x)在[1,+∞)上单调递增.
是奇函数,(a,b,c都是整数),且f(1)=2,f(2)<3,f(x)在[1,+∞)上单调递增.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com