某工厂6年来生产某种产品的总产量C(即前t年产量之和)与时间t(年)的函数关系如图所示,则关于下面的几种说法中正确的是_________.

①前三年中,年产量增长的速度越来越快

②前三年中,年产量增长的速度越来越慢

③后三年中,这种产品的年产量保持不变

④第三年中,这种产品停止生产

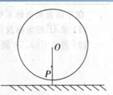    在生活中有很多现象具有周期性，大家学过的三角函数就是描述周期现象的一种重要的数学模型，假设游乐场中的摩天轮匀速旋转，其中心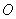距离地面30.5m，半径30m。若从最低点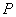处登上摩天轮，从你登上摩天轮开始计时，那么你与地面的距离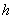将随时间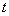变化，并且经过6min到达最高点，请完成下列问题：

    （1）填写表格：

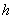    （2）求与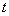之间的函数关系式；

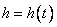    （3）当你在摩天轮上转第一圈，并且距离地面15.5m时，所用时间是多少？当你在摩天轮上转第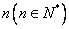圈，并且距离地面15.5m，所用时间是多少？

经济学中有一个用来权衡企业生产能力（简称“产能”）的模型，称为“产能边界”．它表示一个企业在产能最大化的条件下，在一定时期内所能生产的几种产品产量的各种可能的组合．例如，某企业在产能最大化条件下，一定时期内能生产A产品x台和B产品y台，则它们之间形成的函数y=f（x）就是该企业的“产能边界函数”．现假设该企业的“产能边界函数”为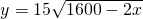（如图）．
（1）试分析该企业的产能边界，分别选用①、②、③中的一个序号填写下表：

点Pi（x，y）对应的产量组合	实际意义
P1（350，450）	③
P2（200，300）
P3（500，400）
P4（408，420）

①这是一种产能未能充分利用的产量组合；
②这是一种生产目标脱离产能实际的产量组合；
③这是一种使产能最大化的产量组合．
（2）假设A产品每台利润为a（a＞0）元，B产品每台利润为A产品每台利润的2倍．在该企业的产能边界条件下，试为该企业决策，应生产A产品和B产品各多少台才能使企业从中获得最大利润？