
题目列表(包括答案和解析)
(06年湖南卷文)(14分)
在m(m≥2)个不同数的排列P1P2…Pn中,若1≤i<j≤m时Pi>Pj(即前面某数大于后面某数),则称Pi与Pj构成一个逆序. 一个排列的全部逆序的总数称为该排列的逆序数. 记排列![]() 的逆序数为an,如排列21的逆序数
的逆序数为an,如排列21的逆序数![]() ,排列321的逆序数
,排列321的逆序数![]() .
.
(Ⅰ)求a4、a5,并写出an的表达式;
(Ⅱ)令![]() ,证明
,证明![]() ,n=1,2,….
,n=1,2,….
已知集合 是正整数
是正整数 的一个排列
的一个排列 ,函数
,函数
 对于
对于 ,定义:
,定义: ,
, ,称
,称 为
为 的满意指数.排列
的满意指数.排列 为排列
为排列 的生成列;排列
的生成列;排列 为排列
为排列 的母列.
的母列.
(Ⅰ)当 时,写出排列
时,写出排列 的生成列及排列
的生成列及排列 的母列;
的母列;
(Ⅱ)证明:若 和
和 为
为 中两个不同排列,则它们的生成列也不同;
中两个不同排列,则它们的生成列也不同;
(Ⅲ)对于 中的排列
中的排列 ,定义变换
,定义变换 :将排列
:将排列 从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:一定可以经过有限次变换
从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:一定可以经过有限次变换 将排列
将排列 变换为各项满意指数均为非负数的排列.
变换为各项满意指数均为非负数的排列.
已知集合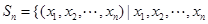 是正整数
是正整数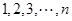 的一个排列
的一个排列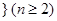 ,函数
,函数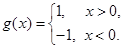 对于
对于 ,定义:
,定义: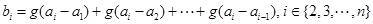 ,
,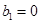 ,称
,称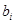 为
为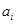 的满意指数.排列
的满意指数.排列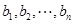 为排列
为排列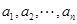 的生成列;排列
的生成列;排列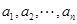 为排列
为排列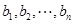 的母列.
的母列.
(Ⅰ)当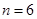 时,写出排列
时,写出排列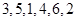 的生成列及排列
的生成列及排列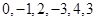 的母列;
的母列;
(Ⅱ)证明:若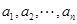 和
和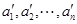 为
为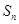 中两个不同排列,则它们的生成列也不同;
中两个不同排列,则它们的生成列也不同;
(Ⅲ)对于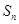 中的排列
中的排列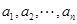 ,定义变换
,定义变换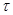 :将排列
:将排列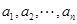 从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:一定可以经过有限次变换
从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:一定可以经过有限次变换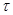 将排列
将排列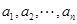 变换为各项满意指数均为非负数的排列.
变换为各项满意指数均为非负数的排列.
(1)求a4、a5,并写出an的表达式;
(2)令bn=![]() +
+![]() ,证明2n<b1+b2+…+bn<2n+3,n=1,2,3….
,证明2n<b1+b2+…+bn<2n+3,n=1,2,3….
排列4321的逆序数a3=6.
(1) 求a4,a5并写出an的表达式;
(2)令bn=![]() ,证明2n<b1+b2+…+bn<2n+3,n=1,2,….
,证明2n<b1+b2+…+bn<2n+3,n=1,2,….
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com