
题目列表(包括答案和解析)
 定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3,},函数y=-x的“特征数”是{0,-1,0}
定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3,},函数y=-x的“特征数”是{0,-1,0}
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 3 |
| 1 |
| 2 |
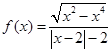 .给出函数
.给出函数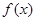 下列性质:①函数的定义域和值域均为
下列性质:①函数的定义域和值域均为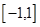 ;②函数的图像关于原点成中心对称;③函数在定义域上单调递增;④
;②函数的图像关于原点成中心对称;③函数在定义域上单调递增;④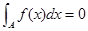 (其中
(其中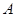 为函数的定义域);⑤
为函数的定义域);⑤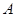 、
、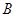 为函数
为函数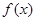 图象上任意不同两点,则
图象上任意不同两点,则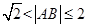 。请写出所有关于函数
。请写出所有关于函数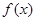 性质正确描述的序号 。
性质正确描述的序号 。函数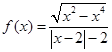 .给出函数
.给出函数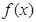 下列性质:⑴函数的定义域和值域均为
下列性质:⑴函数的定义域和值域均为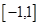 ;⑵函数的图像关于原点成中心对称;⑶函数在定义域上单调递增;⑷
;⑵函数的图像关于原点成中心对称;⑶函数在定义域上单调递增;⑷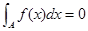 (其中
(其中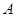 为函数的定义域);⑸
为函数的定义域);⑸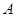 、
、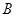 为函数
为函数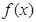 图象上任意不同两点,则
图象上任意不同两点,则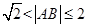 .请写出所有关于函数
.请写出所有关于函数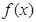 性质正确描述的序号 .
性质正确描述的序号 .
函数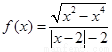 .给出函数
.给出函数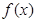 下列性质:⑴函数的定义域和值域均为
下列性质:⑴函数的定义域和值域均为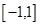 ;⑵函数的图像关于原点成中心对称;⑶函数在定义域上单调递增;⑷
;⑵函数的图像关于原点成中心对称;⑶函数在定义域上单调递增;⑷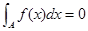 (其中
(其中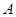 为函数的定义域);⑸
为函数的定义域);⑸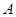 、
、 为函数
为函数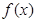 图象上任意不同两点,则
图象上任意不同两点,则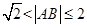 .请写出所有关于函数
.请写出所有关于函数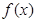 性质正确描述的序号
.
性质正确描述的序号
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com