
题目列表(包括答案和解析)
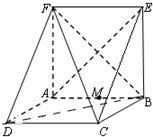 矩形ABCD与矩形ABEF有公共边AB,且平面ABCD⊥平面ABEF,如图,又FD=2,AD=1,EF=
矩形ABCD与矩形ABEF有公共边AB,且平面ABCD⊥平面ABEF,如图,又FD=2,AD=1,EF=| 3 |
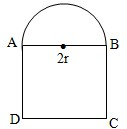 例1:某建材厂要生产一批如图所示的窗框,它由矩形ABCD与以AB为直径的半圆组成,已知窗框的框架的总面积为1平方米,制造矩形ABCD的直线型钢材每米价格为4元,制造半圆的弧形钢材每米价格为6元,设AB=2r,制造每扇窗框的材料价格为S元,把S表示成r的函数,并求S的最小值.
例1:某建材厂要生产一批如图所示的窗框,它由矩形ABCD与以AB为直径的半圆组成,已知窗框的框架的总面积为1平方米,制造矩形ABCD的直线型钢材每米价格为4元,制造半圆的弧形钢材每米价格为6元,设AB=2r,制造每扇窗框的材料价格为S元,把S表示成r的函数,并求S的最小值.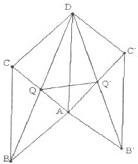 如图,矩形ABCD与矩形AB′C′D全等,且所在平面所成的二面角为a,记两个矩形对角线的交点分别为Q,Q′,AB=a,AD=b.
如图,矩形ABCD与矩形AB′C′D全等,且所在平面所成的二面角为a,记两个矩形对角线的交点分别为Q,Q′,AB=a,AD=b.| 2 |
| π |
| 3 |
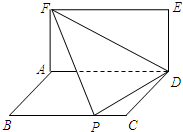 矩形ABCD与矩形ADEF所在的平面互相垂直,将△DEF沿FD翻折,翻折后的点E恰与BC上的点P重合.设AB=1,FA=x(x>1),AD=y,则当x=
矩形ABCD与矩形ADEF所在的平面互相垂直,将△DEF沿FD翻折,翻折后的点E恰与BC上的点P重合.设AB=1,FA=x(x>1),AD=y,则当x=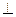 平面ABEF,如图所示,FD
平面ABEF,如图所示,FD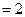 , AD=1, EF=
, AD=1, EF=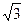 .
.
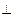 平面FCB;
平面FCB;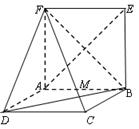
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com