
题目列表(包括答案和解析)
(本小题满分12分)
在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖. 已知教师甲投进每个球的概率都是![]() .
.
(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率;
(Ⅲ)已知教师乙在某场比赛中,6个球中恰好投进了4个球,求教师乙在这场比赛中获奖的概率;教师乙在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗?
.(本小题满分12分)
某科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期限内就攻克技术难题的小组给予奖励.已知此技术难题在攻关期限内被甲小组攻克的概率为 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 .
.
(1)设 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 的分布列及
的分布列及 ;
;
(2)设 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数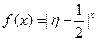 在定义域内单调递增”为事件
在定义域内单调递增”为事件 ,求事件
,求事件 的概率.
的概率.
(本小题满分12分)已知抛物线方程为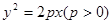
(1)若点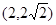 在抛物线上,求抛物线的焦点
在抛物线上,求抛物线的焦点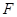 的坐标和准线
的坐标和准线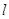 的方程;
的方程;
(2)在(1)的条件下,若过焦点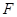 且倾斜角为
且倾斜角为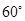 的直线
的直线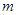 交抛物线于
交抛物线于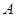 、
、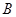 两点,点
两点,点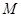 在抛物线的准线
在抛物线的准线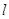 上,直线
上,直线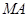 、
、 、
、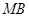 的斜率分别记为
的斜率分别记为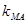 、
、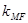 、
、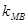 ,
,
求证: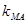 、
、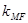 、
、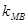 成等差数列;
成等差数列;
(本小题满分12分)
已知点 是区域
是区域 ,(
,( )内的点,目标函数
)内的点,目标函数 ,
, 的最大值记作
的最大值记作 .若数列
.若数列 的前
的前 项和为
项和为 ,
, ,且点(
,且点(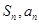 )在直线
)在直线 上.
上.
(Ⅰ)证明:数列 为等比数列;
为等比数列;
(Ⅱ)求数列 的前
的前 项和
项和 .
.
(本小题满分12分) 第11届全国人大五次会议于20 1 2年3月5日至3月1 4日在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和1 4名女记者担任对外翻译工作,调查发现,男、女记者中分别有10人和6人会俄语.
(Ⅰ)根据以上数据完成以下2×2列联表:

并回答能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?
(参考公式:
参考数据:

(Ⅱ)已知会俄语的6名女记者中有4人曾在俄罗斯工作过,若从会俄语的6名女记者中随
机抽取2人做同声翻译,则抽出的2人都在俄罗斯工作过的概率是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com