
题目列表(包括答案和解析)
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
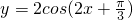 的图象.可以由诱导公式先把它变成y=2sin( ________)然后由y=sinx的图象先向 ________平移 ________个单位,再把各点的纵坐标不变,横坐标变为原来的 ________倍,最后把各点的横坐标不变,纵坐标变为原来的 ________倍,就可以得到
的图象.可以由诱导公式先把它变成y=2sin( ________)然后由y=sinx的图象先向 ________平移 ________个单位,再把各点的纵坐标不变,横坐标变为原来的 ________倍,最后把各点的横坐标不变,纵坐标变为原来的 ________倍,就可以得到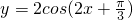 的图象.
的图象.在△ABC中,角A,B,C所对边分别为a,b,c,且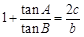 .
.
(Ⅰ)求角A;
(Ⅱ)若m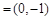 ,n
,n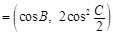 ,试求|m
,试求|m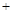 n|的最小值.
n|的最小值.
【解析】(I)把切化成弦,然后根据正弦定理,把等号右边的边的比,转化为对应的角的正弦的比,再借助诱导公式求A.
(II)根据第(I)问求出的A角,然后把C角用B角来表示,再借助向量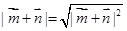 表示成关于角B的函数,然后根据三角函数的知识求最小值即可.
表示成关于角B的函数,然后根据三角函数的知识求最小值即可.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com