练习册

  • 练习册
  • 试题
    3． 如图.在四棱锥P-ABCD中.侧面PAD⊥底面ABCD.侧棱PA＝PD=,底面ABCD为直角梯形.其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.O为AD中点. (Ⅰ)求证:PO⊥平面ABCD, (Ⅱ)求异面直线PB与CD所成角的余弦值, (Ⅲ)求点A到平面PCD的距离. 解法一: (Ⅰ)证明:在△PAD卡中PA＝PD.O为AD中点.所以PO⊥AD. 又侧面PAD⊥底面ABCD.平面PAD∩平面ABCD＝AD.PO平面PAD. 所以PO⊥平面ABCD. (Ⅱ)连结BO.在直角梯形ABCD中.BC∥AD,AD=2AB=2BC. 有OD∥BC且OD＝BC.所以四边形OBCD是平行四边形. 所以OB∥DC. 由(Ⅰ)知PO⊥OB.∠PBO为锐角. 所以∠PBO是异面直线PB与CD所成的角. 因为AD＝2AB＝2BC＝2.在Rt△AOB中.AB＝1.AO＝1.所以OB＝. 在Rt△POA中.因为AP＝.AO＝1.所以OP＝1. 在Rt△PBO中.PB＝, cos∠PBO=, 所以异面直线PB与CD所成的角的余弦值为. 得CD＝OB＝. 在Rt△POC中.PC＝. 所以PC＝CD＝DP.S△PCD=·2=. 又S△= 设点A到平面PCD的距离h. 由VP-ACD=VA-PCD. 得S△ACD·OP＝S△PCD·h. 即×1×1＝××h. 解得h＝. 解法二: (Ⅰ)同解法一. (Ⅱ)以O为坐标原点.的方向分别为x轴.y轴.z轴的正方向.建立空间直角坐标系O-xyz. 则A.B.C. D.P. 所以＝.＝(t.-1.-1). ∞〈.〉=. 所以异面直线PB与CD所成的角的余弦值为. (Ⅲ)设平面PCD的法向量为n＝(x0,y0,x0). 由(Ⅱ)知=.＝. 则 n·＝0.所以 -x0+ x0=0, n·＝0. -x0+ y0=0. 即x0=y0=x0, 取x0=1.得平面的一个法向量为n=. 又=. 从而点A到平面PCD的距离d＝ 【查看更多】

     

    题目列表(包括答案和解析)

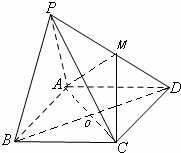    精英家教网如图，在四棱锥P-ABCD中，底面ABCD是矩形．已知AB=3，AD=2，PA=2，PD=2
    		2
    ，∠PAB=60°    ．M是PD的中点．
    （Ⅰ）证明PB∥平面MAC
    （Ⅱ）证明平面PAB⊥平面ABCD
    （Ⅲ）求四棱锥p-ABCD的体积．

    查看答案和解析>>

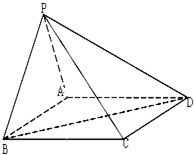    如图，在四棱锥P-ABCD中，底面ABCD是矩形，知AB=3，AD=2，PA=2，PD=2
    		2
    ，∠PAB=60°．
    （1）证明：AD⊥平面PAB；
    （2）求异面直线PC与AD所成的角的余弦值；
    （3）求二面角P-BD-A的大小余弦值．

    查看答案和解析>>

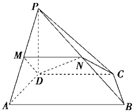    如图，在四棱锥P-ABCD中，PD⊥底面ABCD，AD⊥AB，CD∥AB，AB=
    		2
    AD=2    ，CD=3，直线PA与底面ABCD所成角为60°，点M、N分别是PA，PB的中点．
    （1）求证：MN∥平面PCD；
    （2）求证：四边形MNCD是直角梯形；
    （3）求证：DN⊥平面PCB．

    查看答案和解析>>

    16、如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA⊥PD，底面ABCD是直角梯形，其中BC∥AD，∠BAD=90°，AD=3BC，O是AD上一点．
    （Ⅰ）若CD∥平面PBO，试指出点O的位置；
    （Ⅱ）求证：平面AB⊥平面PCD．

    查看答案和解析>>

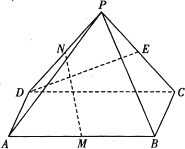    （2011•武汉模拟）如图，在四棱锥P-ABCD中，△PCD为等边三角形，四边形ABCD为矩形，平面PDC丄平面ABCD，M、N、E分别是AB、PD、PC的中点，AB=2AD．
    （Ⅰ）求证DE丄MN；
    （Ⅱ）求二面角B-PA-D的余弦值．

    查看答案和解析>>


    同步练习册答案