
题目列表(包括答案和解析)
[选做题]
A.选修4—1:几何证明选讲
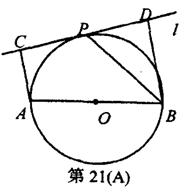
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
(1)l是⊙O的切线;
(2)PB平分∠ABD.
|
 对应的变换将点
对应的变换将点 与
与 分别变换成点
分别变换成点 与
与 .求矩阵
.求矩阵 ;
; 的最大值.
的最大值.[选做题]
A.选修4—1:几何证明选讲
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
(1)l是⊙O的切线;
(2)PB平分∠ABD.

B.选修4—2:矩阵与变换
二阶矩阵 对应的变换将点
对应的变换将点 与
与 分别变换成点
分别变换成点 与
与 .求矩阵
.求矩阵 ;
;
C.选修4—4:坐标系与参数方程
若两条曲线的极坐标方程分别为=l与=2cos(θ+),它们相交于A,B两点,求线
段AB的长.
D.选修4—5:不等式选讲
求函数 的最大值.
的最大值.
|
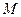 对应的变换将点
对应的变换将点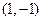 与
与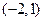 分别变换成点
分别变换成点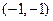 与
与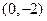 .求矩阵
.求矩阵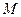 ;
; 的最大值.
的最大值. .
.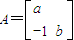 把直线l:y=2x-4变换为直线l′:y=x-12,求a,b的值.
把直线l:y=2x-4变换为直线l′:y=x-12,求a,b的值. =1上的点P到直线l:3x+4y+18=0的距离的最小值.
=1上的点P到直线l:3x+4y+18=0的距离的最小值. ,求x+y+z的最大值.
,求x+y+z的最大值.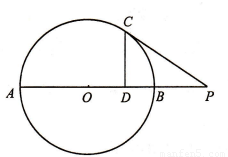
 选做题(在A、B、C、D四小题中只能选做两题,并将选作标记用2B铅笔涂黑,每小题10分,共20分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).
选做题(在A、B、C、D四小题中只能选做两题,并将选作标记用2B铅笔涂黑,每小题10分,共20分,请在答题指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).
|
| π |
| 4 |
| ||
| 2 |
| ab |
| bc |
| ca |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com