
题目列表(包括答案和解析)
若a>0, b>0, 且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于
A. 2 B. 3
C. 6 D. 9
若抛物线C1: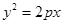 (p >0)的焦点F恰好是双曲线C2:
(p >0)的焦点F恰好是双曲线C2: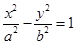 (a>0,b >0)的右焦点,且它们的交点的连线过点F,则双曲线的离心率为
(a>0,b >0)的右焦点,且它们的交点的连线过点F,则双曲线的离心率为
A. B.
B.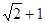 C.
C.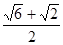 D.
D.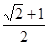
设x,y满足约束条件 ,若目标函数z ="ax+by"
(a>0, b>0)的最大值为8,点P为曲线
,若目标函数z ="ax+by"
(a>0, b>0)的最大值为8,点P为曲线 上动点,则点P到点(a,b)的最小距离为
上动点,则点P到点(a,b)的最小距离为
A.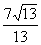 B.O C.
B.O C.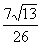 D.1
D.1
设F1,F2是双曲线C,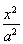 -
-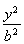 =1(a>0,b>0)的两个焦点.若在C上存在一点P,使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为 .
=1(a>0,b>0)的两个焦点.若在C上存在一点P,使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为 .
. (本小题满分14分)

第21题
设双曲线![]() =1( a > 0, b > 0 )的右顶点为A,P是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP分别交于Q和R两点.
=1( a > 0, b > 0 )的右顶点为A,P是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP分别交于Q和R两点.
(1) 证明:无论P点在什么位置,总有|![]() |2 = |
|2 = |![]() ·
·![]() | ( O为坐标原点);
| ( O为坐标原点);
(2) 若以OP为边长的正方形面积等于双曲线实、虚轴围成的矩形面积,求双曲线离心率的取值范围;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com