
题目列表(包括答案和解析)
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设 ,对于项数为
,对于项数为 的有穷数列
的有穷数列 ,令
,令 为
为 中最大值,称数列
中最大值,称数列 为
为 的“创新数列”.例如数列
的“创新数列”.例如数列 3,5,4,7的创新数列为3,5,5,7.
3,5,4,7的创新数列为3,5,5,7.
考查自然数 的所有排列,将每种排列都视为一个有穷数列
的所有排列,将每种排列都视为一个有穷数列 .
.
(1)若 ,写出创新数列为3,4,4,4的所有数列
,写出创新数列为3,4,4,4的所有数列 ;
;
(2)是否存在数列 的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由.
的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由.
(3)是否存在数列 ,使它的创新数列为等差数列?若存在,求出满足所有条件的数列
,使它的创新数列为等差数列?若存在,求出满足所有条件的数列 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
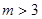 ,对于项数为
,对于项数为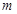 的有穷数列
的有穷数列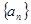 ,令
,令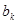 为
为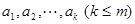 中最大值,称数列
中最大值,称数列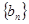 为
为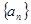 的“创新数列”.例如数列
的“创新数列”.例如数列 3,5,4,7的创新数列为3,5,5,7.
3,5,4,7的创新数列为3,5,5,7.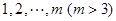 的所有排列,将每种排列都视为一个有穷数列
的所有排列,将每种排列都视为一个有穷数列 .
.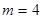 ,写出创新数列为3,4,4,4的所有数列
,写出创新数列为3,4,4,4的所有数列 ;
; 的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由.
的创新数列为等比数列?若存在,求出符合条件的创新数列;若不存在,请说明理由. ,使它的创新数列为等差数列?若存在,求出满足所有条件的数列
,使它的创新数列为等差数列?若存在,求出满足所有条件的数列 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,
第3小题满分8分.
记函数 在区间D上的最大值与最小值分别为
在区间D上的最大值与最小值分别为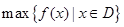 与
与 .设函数
.设函数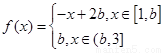 ,
, .
. .
.
(1)若函数 在
在 上单调递减,求
上单调递减,求 的取值范围;
的取值范围;
(2)若 .令
.令 .
.
记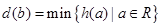 .试写出
.试写出 的表达式,并求
的表达式,并求 ;
;
(3)令 (其中I为
(其中I为 的定义域).若I恰好为
的定义域).若I恰好为 ,求b的取值范围,并求
,求b的取值范围,并求 .
.
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知函数 (
( )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 .
.
(1)求 、
、 的值;
的值;
(2)若不等式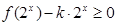 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)若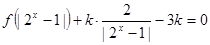 有三个不同的实数解,求实数
有三个不同的实数解,求实数 的取值范围.
的取值范围.
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分5分,第3小题满分9分.
已知数列![]() 是各项均为正数的等差数列,公差为d(d
是各项均为正数的等差数列,公差为d(d ![]() 0).在
0).在![]() 之间和b,c之间共插入
之间和b,c之间共插入![]() 个实数,使得这
个实数,使得这![]() 个数构成等比数列,其公比为q.
个数构成等比数列,其公比为q.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若插入的n个数中,有s个位于a,b之间,t个位于b,c之间,且![]() 都为奇数,试比较s与t的大小,并求插入的n个数的乘积(用
都为奇数,试比较s与t的大小,并求插入的n个数的乘积(用![]() 表示).
表示).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com