
题目列表(包括答案和解析)
从甲、乙,……,等![]() 人中选出
人中选出![]() 名代表,那么(1)甲一定当选,共有 种选法.(2)甲一定不入选,共有 种选法.(3)甲、乙二人至少有一人当选,共有 种选法.
名代表,那么(1)甲一定当选,共有 种选法.(2)甲一定不入选,共有 种选法.(3)甲、乙二人至少有一人当选,共有 种选法.
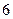 人中选出
人中选出 名代表,那么(1)甲一定当选,共有 种选法.(2)甲一定不入选,共有 种选法.(3)甲、乙二人至少有一人当选,共有 种选法.
名代表,那么(1)甲一定当选,共有 种选法.(2)甲一定不入选,共有 种选法.(3)甲、乙二人至少有一人当选,共有 种选法.为了拓展网络市场,腾讯公司为 用户推出了多款
用户推出了多款 应用,如“
应用,如“ 农场”、“
农场”、“ 音乐”、“
音乐”、“ 读书”等.某校研究性学习小组准备举行一次“
读书”等.某校研究性学习小组准备举行一次“ 使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:[来源:学#科#网Z#X#X#K]
使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:[来源:学#科#网Z#X#X#K]
|
班级 |
一班 |
二班 |
三班 |
四班 |
|
人数 |
2人 |
3人 |
4人 |
1人 |
(1)从这10名学生中随机选出2名,求这2人来自相同班级的概率;
(2) 假设在某时段,三名学生代表甲、乙、丙准备分别从 农场、
农场、 音乐、
音乐、 读书中任意选择一项,他们选择
读书中任意选择一项,他们选择 农场的概率都为
农场的概率都为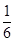 ;选择
;选择 音乐的概率都为
音乐的概率都为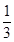 ;选择
;选择 读书的概率都为
读书的概率都为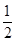 ;他们的选择相互独立.设在该时段这三名学生中选择
;他们的选择相互独立.设在该时段这三名学生中选择 读书的总人数为随机变量
读书的总人数为随机变量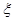 ,求随机变量
,求随机变量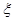 的分布列及数学期望
的分布列及数学期望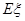 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com