已知函数f(x)=ax²+4(a为非零实数),设函数F(x)=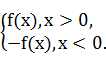
(1)若f(-2)=0,求F(x)的表达式.
(2)在(1)的条件下,解不等式1≤|F(x)|≤2.
(3)设mn<0,m+n>0,试判断F(m)+F(n)能否大于0?

已知函数f(x)＝lnx＋x². (1)若函数g(x)＝f(x)－ax在定义域内为增函数，求实数a的取值范围； (2)在(1)的条件下，若a>1，h(x)＝e^3x－3ae^x，x∈[0，ln2]，求h(x)的极小值； (3)设F(x)＝2f(x)－3x²－kx(k∈R)，若函数F(x)存在两个零点m，n(0<m<n)，且满足2x₀＝m＋n，问：函数F(x)在(x₀，F(x₀))处的切线能否平行于x轴？若能，求出该切线方程，若不能，请说明理由．

(1)若f(-2)=0,求F(x)的表达式;

(2)在(1)的条件下,解不等式1≤|F(x)|≤2;

(3)设mn＜0,m+n＞0,试判断F(m)+F(n)能否大于0?

(文)杭州风景区有一家自行车租车公司,公司设有A、B、C三个营业站,顾客可以从任何一处营业站租车,并在任何一处营业站还车.根据统计发现租车处与还车处有如下的规律性:

①在A站租车者有30%在A站还车,20%在B站还车,50%在C站还车;

②在B站租车者有70%在A站还车,10%在B站还车,20%在C站还车;

③在C站租车者有40%在A站还车,50%在B站还车,10%在C站还车.

记P(XY)表示“某车由X站租出还至Y站的概率”,P(XY)P(YZ)表示“某车由X站租出还至Y站,再由Y站租出还至Z站的概率”.按以上约定的规则,

(1)求P(CC);

(2)求P(AC)P(CB);

(3)设某辆自行车从A站租出,求此车归还至某站再次出租后,回到A站的概率.