（2012•黄州区模拟）2012年春晚歌舞类节目成为春晚顶梁柱，尤其是不少创意组合都被网友称赞很有新意．王力宏和李云迪的钢琴PK，加上背景板的黑白键盘，更被网友称赞是行云流水的感觉．某网站从2012年1月23号到1月30做了持续一周的在线调查，共有n人参加调查，现将数据整理分组如题中表格所示．

序号	年龄分组	组中值mi	频数（人数）	频率（f）
1	[20，25）	22.5	x	s
2	[25，30）	27.5	800	t
3	[30，35）	32.5	y	0.40
4	[35，40）	37.5	1600	0.32
5	[40，45）	42.5	z	0.04

（1）求n及表中x，y，z，s，t的值．
（2）为了对数据进行分析，采用了计算机辅助计算，分析其中一部分计算，见算法流程图，求输出的S值，并说明S的统计意义．
（3）从年龄在[20，30）岁人群中采用分层抽样法抽取6人参加元宵晚会活动，其中选取2人作为代表发言，求选取2名代表中恰有1人年龄在[25，30）岁的概率．

“根据《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20-80mg/100ml（不含80）之间，属于酒后驾车，血液酒精浓度在80mg/100ml（含80）以上时，属醉酒驾车．”某市交警在该市一交通岗前设点对过往的车辆进行抽查，经过一晚的抽查，共查出酒后驾车者60名，图甲是用酒精测试仪对这60 名酒后驾车者血液中酒精浓度进行检测后依所得结果画出的频率分布直方图．
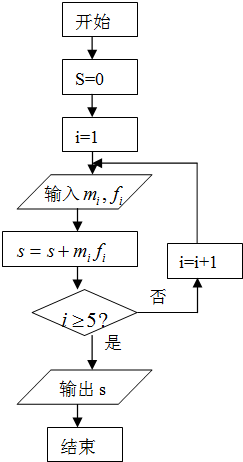
（1）统计方法中，同一组数据常用该组区间的中点值作为代表，图乙的程序框图是对这60名酒后驾车者血液的酒精浓度做进一步的统计，求出图乙输出的S值，并说明S的统计意义；（图乙中数据m_i与f_i分别表示图甲中各组的组中值及频率）
（2）本次行动中，吴、李两位先生都被酒精测试仪测得酒精浓度属于70-90mg/100ml的范围，但他俩坚称没喝那么多，是测试仪不准，交警大队队长决定在被酒精测试仪测得酒精浓度属于70-90mg/100ml范围的酒后驾车者中随机抽出2人抽血检验，ξ为吴、李两位先生被抽中的人数，求ξ的分布列，并求吴、李两位先生至少有1人被抽中的概率；
（3）很多人在喝酒后通过喝茶降解体内酒精浓度，但李时珍就曾指出酒后喝茶伤肾．为研究长期酒后喝茶与肾损伤是否有关，某科研机构采集了统计数据如下表，请你从条件概率的角度给出判断结果，并说明理由．

	没有肾损伤	有肾损伤
长期酒后喝茶	2099	49
酒后不喝茶	7775	42

（2013•韶关二模）以下四个命题
①在一次试卷分析中，从每个试室中抽取第5号考生的成绩进行统计，是简单随机抽样；
②样本数据：3，4，5，6，7的方差为2；
③对于相关系数r，|r|越接近1，则线性相关程度越强；
④通过随机询问110名性别不同的行人，对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查，得到如下列联表：

	男	女	总计
走天桥	40	20	60
走斑马线	20	30	50
总计	60	50	110

附表：

P（K2≥k）	0.05	0.010	0.001
k	3.841	6.635	10.828

由K2=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

可得，k²=

110×(40×30-20×20)

60×50×60×50

=7.8，
则有99%以上的把握认为“选择过马路方式与性别有关”．其中正确的命题序号是．

3、一个年级有12个班，每个班从1-50排学号，为了交流学习经验，要求每班的14参加交流活动，这里运用的抽样方法是（　　）