
题目列表(包括答案和解析)
请认真阅读下列材料:

 “杨辉三角” (1261年)是中国古代重要的数学成就,它比西方的“帕斯卡三角”(1653年)早了300多年(如表1).在“杨辉三角”的基础上德国数学家莱布尼兹发现了下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)
“杨辉三角” (1261年)是中国古代重要的数学成就,它比西方的“帕斯卡三角”(1653年)早了300多年(如表1).在“杨辉三角”的基础上德国数学家莱布尼兹发现了下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)
请回答下列问题:
(I)记 为表1中第n行各个数字之和,求
为表1中第n行各个数字之和,求
 ,并归纳出
,并归纳出 ;
;
(II)根据表2前5行的规律依次写出第6行的数.
 下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)
下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)

 为表1中第n行各个数字之和,求
为表1中第n行各个数字之和,求
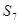 ,并归纳出
,并归纳出 ;
;对对数函数的图象和性质的研究,教材是根据互为反函数的图象特征,由指数函数的图象再作出其关于直线y=x的图象,即得对数函数的图象,在数形结合的数学思想指导下,推得对数函数的性质.请归纳对数函数y=logax(a>0且a≠1)的性质.
| n(n-2) | 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com