
题目列表(包括答案和解析)
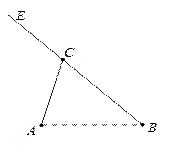
(本小题满分12分) 如图,A,B,C是三个汽车站,AC,BE是直线型公路.已知AB=120 km,∠BAC=75°,∠ABC=45°.有一辆车(称甲车)以每小时96(km)的速度往返于车站A,C之间,到达车站后停留10分钟;另有一辆车(称乙车)以每小时120(km)的速度从车站B开往另一个城市E,途经车 站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
(1)计算A,C两站距 离,及B,C两站距离;(2)若甲、乙两车上各有一名旅客需要交换到对方汽车上,问能否在车站C处利用停留时间交换.(3)求10点时甲、乙两车的距离.(可能用到的参考数据:
离,及B,C两站距离;(2)若甲、乙两车上各有一名旅客需要交换到对方汽车上,问能否在车站C处利用停留时间交换.(3)求10点时甲、乙两车的距离.(可能用到的参考数据: ,
, ,
, ,
, )
)
 站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出. 离,及B,C两站距离;(2)若甲、乙两车上各有一名旅客需要交换到对方汽车上,问能否在车站C处利用停留时间交换.(3)求10点时甲、乙两车的距离.(可能用到的参考数据:
离,及B,C两站距离;(2)若甲、乙两车上各有一名旅客需要交换到对方汽车上,问能否在车站C处利用停留时间交换.(3)求10点时甲、乙两车的距离.(可能用到的参考数据: ,
, ,
, ,
, )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com