甲船由岛出发向北偏东的方向作匀速直线航行，速度为海里∕小时，在甲船从岛出发的同时，乙船从岛正南海里处的岛出发，朝北偏东的方向作匀速直线航行，速度为海里∕小时。

⑴求出发小时时两船相距多少海里？

⑴   两船出发后多长时间相距最近？最近距离为多少海里？

【解析】第一问中根据时间得到出发小时时两船相距的海里为

第二问设时间为t，则

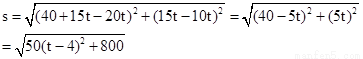
利用二次函数求得最值，

解：⑴依题意有：两船相距

答：出发3小时时两船相距海里                           

⑵两船出发后t小时时相距最近，即

即当t=4时两船最近，最近距离为海里。

已知函数，.

（Ⅰ）若函数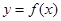依次在处取到极值.求的取值范围；

（Ⅱ）若存在实数，使对任意的，不等式 恒成立.求正整数的最大值.

【解析】第一问中利用导数在在处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。

第二问中，利用存在实数，使对任意的，不等式 恒成立转化为，恒成立，分离参数法求解得到范围。

解：（1）

①

（2）不等式 ，即，即.

转化为存在实数，使对任意的，不等式恒成立.

即不等式在上恒成立.

即不等式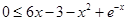在上恒成立.

设，则.

设，则，因为，有.

故在区间上是减函数。又

故存在，使得.

当时，有，当时，有.

从而在区间上递增，在区间上递减.

又[来源:]

所以当时，恒有；当时，恒有；

故使命题成立的正整数m的最大值为5

已知函数.

(Ⅰ)当a = 3时,求不等式的解集;

(Ⅱ)若对恒成立,求实数a的取值范围.

已知命题方程在上有解；命题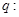不等式恒成立，若命题“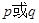”是假命题，求的取值范围．