
题目列表(包括答案和解析)
 在平面直角坐标系xOy中,已知⊙C1:(x+3)2+(y-1)2=4和⊙C2:(x-5)2+(y-1)2=4
在平面直角坐标系xOy中,已知⊙C1:(x+3)2+(y-1)2=4和⊙C2:(x-5)2+(y-1)2=4| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
 (2009宁夏海南卷理) 如图,正方体
(2009宁夏海南卷理) 如图,正方体![]() 的棱线长为1,线段
的棱线长为1,线段![]() 上有两个动点E,F,且
上有两个动点E,F,且![]() ,则下列结论中错误的是
,则下列结论中错误的是
(A)![]()
(B)![]()
(C)三棱锥![]() 的体积为定值
的体积为定值
(D)异面直线![]() 所成的角为定值
所成的角为定值
已知集合M={直线的倾斜角},集合N={两条异面直线所成的角},集合P={直线与平面所成的角},则下列结论中正确的个数为 ( )
①(M∩N)∩P=(0,![]()
![]() ②(M∩N)∪P=(0,π
②(M∩N)∪P=(0,π![]()
③(M∩N)∪P=(0,![]()
![]() ④(M∩N)∩P=(0,
④(M∩N)∩P=(0,![]() )
)
A.4个 B.3个 C.2个 D.1个
正方体 的棱线长为1,面对角线
的棱线长为1,面对角线 上有两个动点E,F,且
上有两个动点E,F,且 ,则下列四个结论中①
,则下列四个结论中① ②
②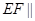 平面
平面 ③三棱锥
③三棱锥 的体积为定值 ④异面直线
的体积为定值 ④异面直线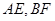 所成的角为定值,其中正确的个数是
所成的角为定值,其中正确的个数是
A.1 B.2 C.3 D.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com