
题目列表(包括答案和解析)
| |||||||||||||||
用 代表红球,
代表红球,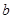 代表蓝球,
代表蓝球,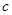 代表黑球,由加法原理及乘法原理,从1个红球和1个篮球中取出若干个球的所有取法可由
代表黑球,由加法原理及乘法原理,从1个红球和1个篮球中取出若干个球的所有取法可由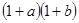 的展开式
的展开式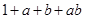 表示出来,如:“1”表示一个球都不取、“
表示出来,如:“1”表示一个球都不取、“ ”表示取出一个红球,面“
”表示取出一个红球,面“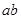 ”用表示把红球和篮球都取出来.以此类推,下列各式中,其展开式可用来表示从5个无区别的红球、5个无区别的蓝球、5个有区别的黑球中取出若干个球,且所有的篮球都取出或都不取出的所有取法的是
”用表示把红球和篮球都取出来.以此类推,下列各式中,其展开式可用来表示从5个无区别的红球、5个无区别的蓝球、5个有区别的黑球中取出若干个球,且所有的篮球都取出或都不取出的所有取法的是
A.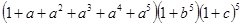 |
B.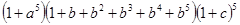 |
C.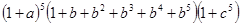 |
D.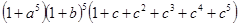 |
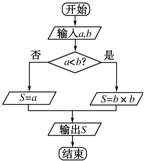 在实数的原有运算法则中,我们补充定义新运算“⊕”,其中S=a?b的运算原理如图所示,则集合{y|y=(1⊕x)•x-(2⊕x),x∈[-2,2]}(注:“•”和“-”仍为通常的乘法和减法)的最大元素是( )
在实数的原有运算法则中,我们补充定义新运算“⊕”,其中S=a?b的运算原理如图所示,则集合{y|y=(1⊕x)•x-(2⊕x),x∈[-2,2]}(注:“•”和“-”仍为通常的乘法和减法)的最大元素是( )解下列各题,需要用分类加法计数原理的是
M和N都是有限集合,求M∪N元素的个数
有4个小组,人数分别为12,12,10,10,从中选1人参加作文比赛,求不同的选法
有4个小组,人数分别为12,12,10,10,每小组选派1人参加座谈会,求不同的选法
已知x∈{1,2,3},y∈{2,3,4},计算M(x,y)能表示多少个不同的点
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com