
题目列表(包括答案和解析)
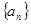 的前
的前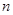 项的和为
项的和为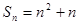 ,
,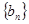 是等比数列,且
是等比数列,且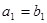 ,
,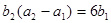 。
。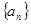 和
和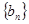 的通项公式;
的通项公式;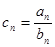 ,求数列
,求数列 的前
的前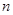 项的和
项的和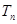 。
。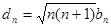 ,数列
,数列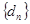 的前
的前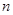 项的和为
项的和为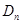 ,求证:
,求证: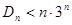 .
.已知数列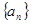 的前
的前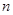 项的和为
项的和为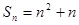 ,
,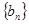 是等比数列,且
是等比数列,且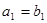 ,
,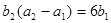 。
。
⑴求数列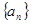 和
和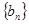 的通项公式;
的通项公式;
⑵设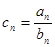 ,求数列
,求数列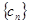 的前
的前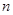 项的和
项的和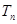 。
。
⑴ 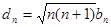 ,数列
,数列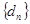 的前
的前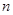 项的和为
项的和为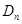 ,求证:
,求证: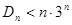 .
.
【解析】第一问利用数列
依题意有:当n=1时,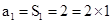 ;
;
当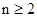 时,
时,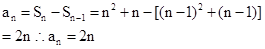
第二问中,利用由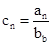 得:
得: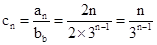 ,然后借助于错位相减法
,然后借助于错位相减法
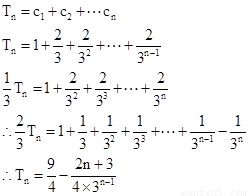
第三问中
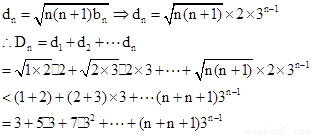
结合均值不等式放缩得到证明。
(12分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() (
(![]() 为正整数)
为正整数)
(I)求数列![]() 的通项公式;
的通项公式;
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,点
,点![]() 都在函数
都在函数![]() 的图像上.
的图像上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,且数列
,且数列![]() 是等差数列,求非零常数
是等差数列,求非零常数![]() 的值;
的值;
(3)设![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,求使得
项和,求使得![]() 对所有
对所有![]() 都成立的最小正整数
都成立的最小正整数![]() .
.
已知数列![]()
![]()
![]() 的前
的前![]() 项和为
项和为![]() ,点列
,点列![]()
![]() ,
,![]()
![]() 在函数
在函数![]()
![]() =
=![]() 的图像上.数列
的图像上.数列![]()
![]()
![]() 满足:对任意的正整数
满足:对任意的正整数![]() 都有0<
都有0<![]() <
<![]() ,且
,且![]() =2成立,则数列
=2成立,则数列![]()
![]()
![]() 可能的一个通项公式是 .
可能的一个通项公式是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com