（09年日照一模文）（12分）

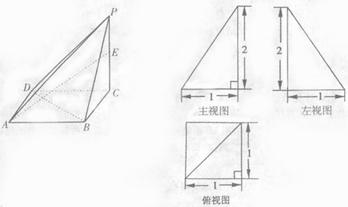
已知四棱锥的三视图如下。

（I）求四棱锥的体积；

（Ⅱ）若是侧棱的中点，求证：平面；

（Ⅲ）若是侧棱上的动点，不论点在何位置，是否都有？证明你的结论。

（09年日照一模文）（12分）

已知函数。

（I）若函数在处有极值-6，求的单调递减区间；

（Ⅱ）若的导数对都有求的范围。

（09年日照一模文）已知向量=（2，2），，则向量的模的最大值是

     A．3         B．      C．      D．18

（08年西工大附中一模理） 已知向量与的夹角为，，，则等于（     ）

      A.5　　　　     B.4　　　　      C.3　　　　     D.1

（08年雅礼中学一模理）已知平面α、β和直线m，给出条件：①m∥α；②m⊥α；③；④α⊥β；⑤α∥β.

（）当满足条件           时，m∥β；

（）当满足条件           时，m⊥β　 （注意：只要填条件中的序号）