
题目列表(包括答案和解析)
若某产品的直径长与标准值的差的绝对值不超过1mm 时,则视为合格品,否则视为不合格品。在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品。计算这50件不合格品的直径长与标准值的差(单位:mm), 将所得数据分组,得到如下频率分布表:
|
分组 |
频数 |
频率 |
|
[-3, -2) |
|
0.10 |
|
[-2, -1) |
8 |
|
|
(1,2] |
|
0.50 |
|
(2,3] |
10 |
|
|
(3,4] |
|
|
|
合计 |
50 |
1.00 |
(Ⅰ)将上面表格中缺少的数据填在答题卡的相应位置;
(Ⅱ)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率;
(Ⅲ)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品。据此估算这批产品中的合格品的件数。
【解析】(Ⅰ)
|
分组 |
频数 |
频率 |
|
[-3, -2) |
5 |
0.10 |
|
[-2, -1) |
8 |
0.16 |
|
(1,2] |
25 |
0.50 |
|
(2,3] |
10 |
0.2 |
|
(3,4] |
2 |
0.04 |
|
合计 |
50 |
1.00 |
(Ⅱ)根据频率分布表可知,落在区间(1,3]内频数为35,故所求概率为0.7.
(Ⅲ)由题可知不合格的概率为 0.01,故可求得这批产品总共有2000,故合格的产品有1980件。
0.01,故可求得这批产品总共有2000,故合格的产品有1980件。
从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( )
(A)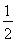 (B)
(B)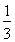 (C)
(C)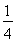 (D)
(D)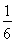
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1;
③在某项测量中,测量结果 服从正态分布
服从正态分布
 .若
.若 在(0,1)内取值的概率为0.4,则
在(0,1)内取值的概率为0.4,则 在(0,2)内取值的概率为0.8 ;
在(0,2)内取值的概率为0.8 ;
④对分类变量X与Y的随机变量K2的观测值k来说,k越小,判断“X与Y有关系”的把握程度越大.
其中真命题的个数为( )
A.1 B.2 C.3 D.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com