
题目列表(包括答案和解析)
| 1 |
| a |
| 2 |
| b |
| A、2 | B、4 | C、6 | D、8 |
(本小题满分l 2分)某书商为提高某套丛书的销量,准备举办一场展销会.据市场调查,当每套丛书售价定为x元时,销售量可达到15一O.1x万套.现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为l0.假设不计其它成本,即销售每套丛书的利润 = 售价 一 供货价格.问:
(I)每套丛书定价为100元时,书商能获得的总利润是多少万元?
(Ⅱ)每套丛书定价为多少元时,单套丛书的利润最大?
已知正项数列 的前n项和
的前n项和 满足:
满足: ,
,
(1)求数列 的通项
的通项 和前n项和
和前n项和 ;
;
(2)求数列 的前n项和
的前n项和 ;
;
(3)证明:不等式  对任意的
对任意的 ,
, 都成立.
都成立.
【解析】第一问中,由于 所以
所以
两式作差 ,然后得到
,然后得到
从而 得到结论
得到结论
第二问中, 利用裂项求和的思想得到结论。
利用裂项求和的思想得到结论。
第三问中,

又
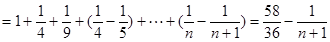
结合放缩法得到。
解:(1)∵ ∴
∴
∴
∴ ∴
∴  ………2分
………2分
又∵正项数列 ,∴
,∴ ∴
∴
又n=1时,
∴ ∴数列
∴数列 是以1为首项,2为公差的等差数列……………3分
是以1为首项,2为公差的等差数列……………3分
∴ …………………4分
…………………4分
∴ …………………5分
…………………5分
(2) …………………6分
…………………6分
∴
 …………………9分
…………………9分
(3)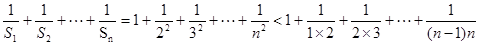
 …………………12分
…………………12分
又

 ,
,
∴不等式  对任意的
对任意的 ,
, 都成立.
都成立.
(本小题满分1 2分)
如图,四边形ABCD中,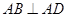 ,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD
,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD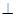 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.
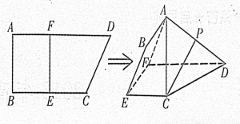
( I )当E为BC中点时,求证:CP//平面ABEF
(Ⅱ)设BE=x,问当x为何值时,三棱锥A-CDF的体积有最大值?并求出这个最大值。
已知函数 , 其中
, 其中 .
.
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,求曲线
时,求曲线 的单调区间与极值.
的单调区间与极值.
【解析】第一问中利用当 时,
时, ,
,
 ,得到切线方程
,得到切线方程
第二问中,

对a分情况讨论,确定单调性和极值问题。
解: (1) 当 时,
时, ,
,
 ………………………….2分
………………………….2分

 切线方程为:
切线方程为:  …………………………..5分
…………………………..5分
(2) 
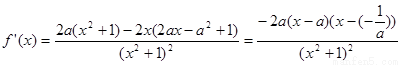 …….7
…….7 分
分
分类: 当 时, 很显然
时, 很显然
 的单调增区间为:
的单调增区间为:  单调减区间:
单调减区间:  ,
,
 ,
,  ………… 11分
………… 11分
当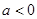 时
时 的单调减区间:
的单调减区间:  单调增区间:
单调增区间: 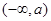 ,
,

 ,
, 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com