
题目列表(包括答案和解析)
在△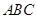 中,∠
中,∠ ,∠
,∠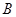 ,∠
,∠ 的对边分别是
的对边分别是 ,且
,且
 .
.
(1)求∠ 的大小;(2)若
的大小;(2)若 ,
, ,求
,求 和
和 的值.
的值.
【解析】第一问利用余弦定理得到
 第二问
第二问
(2) 由条件可得 
将  代入 得 bc=2
代入 得 bc=2
解得 b=1,c=2 或 b=2,c=1 .
解:(Ⅰ)设![]() :
:![]()
![]() ,其半焦距为
,其半焦距为![]()
![]() .则
.则![]() :
:![]() .
.
由条件知![]() ,得
,得![]() .
.
![]() 的右准线方程为
的右准线方程为![]() ,即
,即![]() .
.
![]() 的准线方程为
的准线方程为![]() .
.
由条件知![]() , 所以
, 所以![]() ,故
,故![]() ,
,![]() .
.
从而![]() :
:![]() ,
, ![]() :
:![]() .
.
(Ⅱ)由题设知![]() :
:![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() .
.
由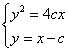 ,得
,得![]() ,所以
,所以![]() .
.
而![]() ,由条件
,由条件![]() ,得
,得![]() .
.
由(Ⅰ)得![]() ,
,![]() .从而,
.从而,![]() :
:![]() ,即
,即![]() .
.
由 ,得
,得![]() .所以
.所以![]() ,
,![]() .
.
故![]() .
.
设椭圆 的左、右顶点分别为
的左、右顶点分别为 ,点
,点 在椭圆上且异于
在椭圆上且异于 两点,
两点, 为坐标原点.
为坐标原点.
(Ⅰ)若直线 与
与 的斜率之积为
的斜率之积为 ,求椭圆的离心率;
,求椭圆的离心率;
(Ⅱ)若 ,证明直线
,证明直线 的斜率
的斜率
 满足
满足
【解析】(1)解:设点P的坐标为 .由题意,有
.由题意,有 ①
①
由 ,得
,得 ,
,
由 ,可得
,可得 ,代入①并整理得
,代入①并整理得
由于 ,故
,故 .于是
.于是 ,所以椭圆的离心率
,所以椭圆的离心率
(2)证明:(方法一)
依题意,直线OP的方程为 ,设点P的坐标为
,设点P的坐标为 .
.
由条件得 消去
消去 并整理得
并整理得 ②
②
由 ,
, 及
及 ,
,
得 .
.
整理得 .而
.而 ,于是
,于是 ,代入②,
,代入②,
整理得
由 ,故
,故 ,因此
,因此 .
.
所以 .
.
(方法二)
依题意,直线OP的方程为 ,设点P的坐标为
,设点P的坐标为 .
.
由P在椭圆上,有
因为 ,
, ,所以
,所以 ,即
,即 ③
③
由 ,
, ,得
,得 整理得
整理得 .
.
于是 ,代入③,
,代入③,
整理得
解得 ,
,
所以 .
.
设函数y=f(x)在区间[0,1]上的图象是连续不断的一条曲线,且恒有0≤f(x)≤1,可以用随机模拟方法近似计算由曲线y=f(x)及直线x=0,x=1,y=0所围成部分的面积S.先产生两组(每组N个)区间[0,1]上的均匀随机数x1,x2,…,xN和y1,y2,…,yN,由此得到N个点(xi,yi)(i=1,2,…,N).再数出其中满足yi≤![]() f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得S的近似值为 .
f(xi)(i=1,2,…,N)的点数N1,那么由随机模拟方法可得S的近似值为 .
设定义在(0,+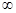 )上的函数
)上的函数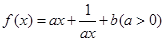
(Ⅰ)求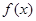 的最小值;
的最小值;
(Ⅱ)若曲线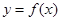 在点
在点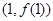 处的切线方程为
处的切线方程为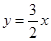 ,求
,求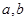 的值。
的值。
【解析】 (Ⅰ)因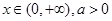 ,故
,故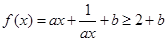 ,取等号的条件是
,取等号的条件是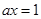 ,即
,即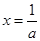 。
。
(Ⅱ)因 ,由
,由 ,求得
,求得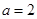 ,又由
,又由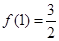 ,可得
,可得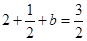 ,解得
,解得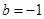
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com