（8分） 抛掷骰子，是大家非常熟悉的日常游戏了．

某公司决定以此玩抛掷（两颗）骰子的游戏，来搞一个大型的促销活动——“轻轻松松抛骰子，欢欢乐乐拿礼券”．

方案1：总点数是几就送礼券几十元．

方案2：总点数为中间数7时的礼券最多，为120元；以此为基准，总点数每减少或增加1，礼券减少20元．

方案3  总点数为2和12时的礼券最多，都为120元；点数从2到7递增或从12到7递减时，礼券都依次减少20元．

如果你是该公司老总，你准备怎样去选择促销方案?请你对以上三种方案给出裁决．

某俱乐部举行迎圣诞活动，每位会员交50元活动费，可享受20元的消费，并参加一次游戏：掷两颗正方体骰子，点数之和为12点获一等奖，奖价值为a元的奖品；点数之和为11或10点获二等奖，奖价值为100元的奖品；点数之和为9或8点获三等奖，奖价值为30元的奖品；点数之和小于8点的不得奖．求：
（Ⅰ）同行的三位会员一人获一等奖、两人获二等奖的概率；
（Ⅱ）如该俱乐部在游戏环节不亏也不赢利，求a的值．

一台机器使用的时间较长，但还可以使用，它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，下表为抽样试验的结果：

（1）利用散点图或相关系数r的大小判断变量y对x是否线性相关？为什么？

（2）如果y对x有线性相关关系，求回归直线方程；

（3）若实际生产中，允许每小时的产品中有缺点的零件最多为10个，那么机器的运转速度应控制在什么范围内？（最后结果精确到0.001．参考数据：，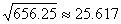

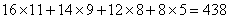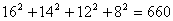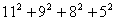，，=291）．