
题目列表(包括答案和解析)
(本小题满分14分)
已知定点A(1,0)和定直线x=-1的两个动点E、F,满足AE⊥AF,动点P满足EP∥OA,FO∥OP(其中O为坐标原点).
(1)求动点P的轨迹C的方程;
(2)过点B(0,2)的直线l与(1)中轨迹C相交于两个不同的点M、N,若∠MAN为钝角,求直线l的斜率的取值范围;
(3)过点T(-1,0)作直线m与(1)中的轨迹C交于两点G、H,问在x轴上是否存在一点D,使△DGH为等边三角形;若存在,试求出点D的坐标;若不存在,请说明理由.
(本小题满分14分) 已知函数f (x)=ex-k-x,其中x∈R. (1)当k=0时,若g(x)=![]() 定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
(本小题满分14分) 已知函数f (x)=ex-k-x,其中x∈R. (1)当k=0时,若g(x)=![]() 定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
 定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.(本小题满分14分)
本题是选作题,考生只能选做其中两个小题.三个小题都作答的,以前两个小题计算得分。
①选修4-4《坐标系与参数方程》选做题(本小题满分7分)
已知曲线C的参数方程是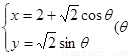 为参数),且曲线C与直线
为参数),且曲线C与直线 =0相交于两点A、B求弦AB的长。
=0相交于两点A、B求弦AB的长。
②选修4-2《矩阵与变换》选做题(本小题满分7分)
已知矩阵 的一个特征值为
的一个特征值为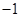 ,它对应的一个特征向量
,它对应的一个特征向量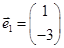 。
。
(Ⅰ)求矩阵M;
(Ⅱ)点P(1, 1)经过矩阵M所对应的变换,得到点Q,求点Q的坐标。
③选修4-5《不等式选讲》选做题(本小题满分7分)
函数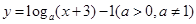 的图象恒过定点
的图象恒过定点 ,若点
,若点 在直
在直 线
线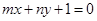 上,其中
上,其中
 ,求
,求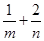 的最小值。
的最小值。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com