(本题满分14分)

如图,圆锥的顶点是S，底面中心为O.OC是与底面直径AB垂直的一条半径，D是母线SC的中点.

（1）求证：BC与SA不可能垂直.

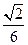（2）设圆锥的高为4，异面直线AD与BC所成角的余弦值为，求圆锥的体积.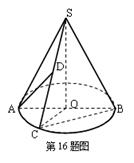

 （本题满分14分，第（1）题6分，第（2）题8分）

如图：圆锥的顶点是S，底面中心为O。OC是与底面直径AB垂直的一条半径，D是母线SC的中点。

   （1）求证：BC与SA不可能垂直；

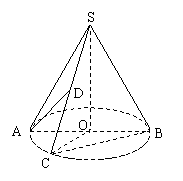   （2）设圆锥的高为4，异面直线AD与BC所成角为，求圆锥的体积。

（本小题满分14分）

如图，有一块半径为2的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底AB是圆O的直径，上底CD的端点在圆周上.

（1）求梯形ABCD的周长y与腰长x间的函数解析式，并求出它的定义域；

（2）求梯形ABCD的周长y的最大值.

（本小题满分14分）

如图，ADB为半圆，AB为半圆直径，O为半圆圆心，且OD⊥AB，Q为线段OD的中点，已知|AB|=4，曲线C过Q点，动点P在曲线C上运动且保持|PA|+|PB|的值不变。

   （I）建立适当的平面直角坐标系，求曲线C的方程；

   （II）过点B的直线l与曲线C交于M、N两点，与OD所在直线交于E点，

        为定值。