练习册

  • 练习册
  • 试题
    B [命题意图]本小题主要考查诱导公式.同角三角函数关系式等三角函数知识.并突出了弦切互化这一转化思想的应用. [解析],所以 (3)若变量满足约束条件则的最大值为 2 (D)1 【查看更多】

     

    题目列表(包括答案和解析)

    平面直角坐标系xOy中，已知A1（x1，y1），A2（x2，y2），…，An（xn，yn）是直线l：y=kx+b上的n个点
    （n∈N*，k、b均为非零常数）．
    （1）若数列{xn}成等差数列，求证：数列{yn}也成等差数列；
    （2）若点P是直线l上一点，且
    OP
    =a1
    OA1
    +a2
    OA2
    ，求a1+a2的值；
    （3）若点P满足
    OP
    =a1
    OA1
    +a2
    OA2
    +…+an
    OAn
    ，我们称
    OP
    是向量
    OA1
    ，
    OA2
    ，…，
    OAn
    的线性组合，{an}是该线性组合的系数数列．当
    OP
    是向量
    OA1
    ，
    OA2
    ，…，
    OAn
    的线性组合时，请参考以下线索：
    ①系数数列{an}需满足怎样的条件，点P会落在直线l上？
    ②若点P落在直线l上，系数数列{an}会满足怎样的结论？
    ③能否根据你给出的系数数列{an}满足的条件，确定在直线l上的点P的个数或坐标？
    试提出一个相关命题（或猜想）并开展研究，写出你的研究过程．[本小题将根据你提出的命题（或猜想）的完备程度和研究过程中体现的思维层次，给予不同的评分]．

    查看答案和解析>>

    （2009湖南卷文）（本小题满分13分）

    对于数列,若存在常数M＞0,对任意的，恒有

    ,            

    则称数列为数列.

    （Ⅰ）首项为1，公比为的等比数列是否为B-数列？请说明理由;

    （Ⅱ）设是数列的前n项和.给出下列两组判断：

    A组：①数列是B-数列,      ②数列不是B-数列;

    B组：③数列是B-数列,      ④数列不是B-数列.

    请以其中一组中的一个论断为条件，另一组中的一个论断为结论组成一个命题.

    判断所给命题的真假，并证明你的结论；

    (Ⅲ)若数列是B-数列，证明：数列也是B-数列。

    查看答案和解析>>

    （本小题满分12分）一个容量为M的样本数据，其频率分布表如下．

    （Ⅰ）表中a=   　   ，b =  　    ；

    （Ⅱ）画出频率分布直方图；

    （Ⅲ）用频率分布直方图，求出总体的众数及平均数的估计值．

    频率分布表                               

    分组

    频数

    频率

    频率/组距

    (10,20]

    2

    0.10

    0.010

    (20,30]

    3

    0.15

    0.015

    (30,40]

    4

    0.20

    0.020

    (40,50]

    a

    b

    0.025

    (50,60]

    4

    0.20

    0.020

    (60, 70]

    2

    0.10

    0.010

     

     

     

     

     

     

     

     

    频率分布直方图

     

    查看答案和解析>>

    （本小题满分14分）
    (1)已知等差数列{an}的前n项和为Sn，若m+n=s+t(m,n,s,t∈N*，且m≠n,s≠t)，证明；= ；
    (2)注意到(1)中Sn与n的函数关系，我们得到命题：设抛物线x2=2py(p>0)的图像上有不同的四点A，B，C，D，若xA，xB，xC，xD分别是这四点的横坐标，且xA+xB=xC+xD，则AB∥CD，判定这个命题的真假，并证明你的结论
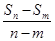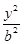    (3)我们知道椭圆和抛物线都是圆锥曲线，根据(2)中的结论，对椭圆+ =1(a>b>0)提出一个有深度的结论，并证明之.

    查看答案和解析>>

    (本小题满分12分) 已知椭圆E：=1（a＞b＞o）的离心率e=，且经过点（,1），O为坐标原点。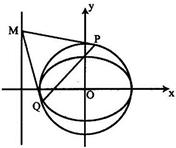

    （Ⅰ）求椭圆E的标准方程；
    　（Ⅱ）圆O是以椭圆E的长轴为直径的圆，M是直线x=－4在x轴上方的一点，过M作圆O的两条切线，切点分别为P、Q，当∠PMQ=60°时，求直线PQ的方程.

    查看答案和解析>>


    同步练习册答案