
题目列表(包括答案和解析)
(本题满分12分)
我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的。某市用水收费标准是:水费=基本费+超额费+定额损耗费,且有如下三条规定:
①若每月用水量不超过最低限量 立方米时,只付基本费9元和每户每月定额损耗费
立方米时,只付基本费9元和每户每月定额损耗费 元;
元;
②若每月用水量超过 立方米时,除了付基本费9元和定额损耗费外,超过部分每立方米付
立方米时,除了付基本费9元和定额损耗费外,超过部分每立方米付 元的超额费;
元的超额费;
③每户每月定额损耗费 不超过5元。
不超过5元。
(1) 求每户每月水费 (元)与月用水量
(元)与月用水量 (立方米)的函数关系式;
(立方米)的函数关系式;
(2) 该市一家庭今年第一季度每月的用水量和支付的费用如下表所示:
|
月份 |
用水量(立方米) |
水费(元) |
|
一 |
4 |
17 |
|
二 |
5 |
23 |
|
三 |
2.5 |
11 |
试分析该家庭今年一、二、三各月份的用水量是否超过最低限量,并求 的值。
的值。
(本题满分12分)探究函数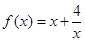 ,
,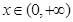 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时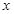 的值,列表如下:
的值,列表如下:
|
|
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
|
|
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.102 |
4.24 |
4.3 |
5 |
5.8 |
7.57 |
… |
请观察表中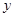 值随
值随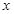 值变化的特点,完成下列问题:
值变化的特点,完成下列问题:
(1) 当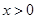 时,
时,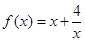 在区间
在区间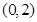 上递减,在区间 上递增;
上递减,在区间 上递增;
所以,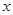 =
时,
=
时, 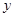 取到最小值为
;
取到最小值为
;
(2) 由此可推断,当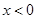 时,
时,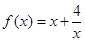 有最
值为 ,此时
有最
值为 ,此时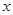 =
;
=
;
(3) 证明: 函数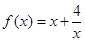 在区间
在区间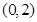 上递减;
上递减;
(4) 若方程 在
在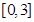 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数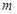 的取值范围。
的取值范围。
(本题满分12分)为了了解某年段1000名学生的百米成绩情况,随机抽取了若
干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组
[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如
图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.

(本题满分12分)
 某校高二(17)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
某校高二(17)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:

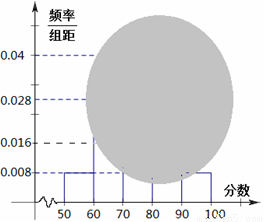
(1)求全班人数;
(2)求分数在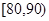 之间的人数;并计算频率分布直方图中
之间的人数;并计算频率分布直方图中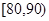 间的矩形的高;
间的矩形的高;
(3)若要从分数在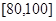 之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在
之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在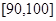 之间的概率.
之间的概率.
(本题满分12分)为了了解某年段1000名学生的百米成绩情况,随机抽取了若
干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组
[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如
图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.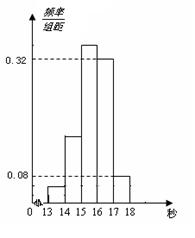
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com