
题目列表(包括答案和解析)
如图,在长方体![]() 中,点
中,点![]() 分别在
分别在![]() 上,且
上,且![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)若规定两个平面所成的角是这两个平面所组成的二面角中的锐角(或直角),则在空间有定理:若两条直线分别垂直于两个平面,则这两条直线所成的角与这两个平面所成角相等,试根据上述定理,在![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.

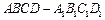 中,点
中,点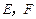 分别在
分别在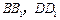 上,且
上,且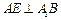 ,
,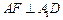 .
.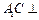 平面
平面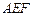 ;
;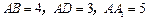 时,求平面
时,求平面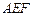 与平面
与平面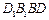 所成角的大小.
所成角的大小.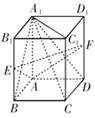
(04年天津卷)如图,在长方体![]() 中,
中,
![]() ,分别过BC、
,分别过BC、
![]() 的两个平行截面将长方体分成
的两个平行截面将长方体分成
三部分,其体积分别记为![]() ,
,
![]() 。若
。若![]() ,则截面
,则截面![]() 的面积为
的面积为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
|
(08年温州八校适应性考试三) 如图,在长方体![]() 中,
中,![]() ,分别过
,分别过![]() 的两个平行截面将长方体分成三部分,其体积分别记为
的两个平行截面将长方体分成三部分,其体积分别记为![]()
若![]() ,则截面
,则截面![]() 的面积 .
的面积 .
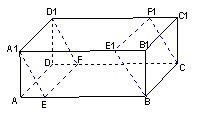
 如图,在长方体中,AB=AD=2
如图,在长方体中,AB=AD=2| 3 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com