
题目列表(包括答案和解析)
| 5 |
| π |
| 4 |
| a |
| b |
| c |
 (其中tanθ=2,θ为锐角)作平行于
(其中tanθ=2,θ为锐角)作平行于 的直线l与曲线分别交于B,C.
的直线l与曲线分别交于B,C. ;
;选择题
(1)
已知全集U=R,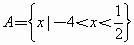 ,B={x|x≤-4},
,B={x|x≤-4}, ,则集合C=
,则集合C=
[
]|
A .A∩B |
B .A∪B |
|
C . |
D . |
(2)
对于全集U的子集M,N,若M是N的真子集,则下列集合中必为空集的是[
]|
A .( |
B .M∩( |
|
C .( |
D .M∩N |
选择题
(1)
集合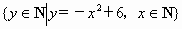 的真子集的个数是
的真子集的个数是
[
]|
A .9 |
B .8 |
C .7 |
D .6 |
(2)
下列表示①{0}=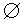 ,②
,②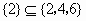 ,③
,③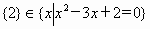 ,④
,④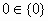 中,错误的是
中,错误的是
[
]|
A .①② |
B .①③ |
C .②④ |
D .②③ |
选择题
(1)
下列集合中,不是方程(x+1)(x-2)(x-3)=0的解集的集合是[
]|
A .{-1,2,3} |
B .{3,-1,2} |
|
C .{x|(x+1)(x-2)(x-3)=0} |
D .{(-1,2,3)} |
(2)
下列结论中,不正确的是[
]|
A . |
B . |
|
C . |
D . |
(3)
已知集合M={x∈N|x=8-m,m∈N},则集合M中的元素的个数为[
]|
A .7 |
B .8 |
C .9 |
D .10 |
(4)
集合{x∈N|-4<x-1<4,且x≠1}的真子集的个数是[
]|
A .32 |
B .31 |
C .16 |
D .15 |
(5)
已知全集U={x∈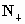 |-2<x<9},M={3,4,5},P={1,3,6},那么{2,7,8}是
|-2<x<9},M={3,4,5},P={1,3,6},那么{2,7,8}是
[
]|
A .M∪P |
B .M∩P |
|
C .( |
D .( |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com