
题目列表(包括答案和解析)
如图,矩形ABCD中,|AB|=2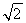 ,|BC|=2.E,F,G,H分别是矩形四条边的中点,分别以HF,EG所在的直线为x轴,y轴建立平面直角坐标系,已知
,|BC|=2.E,F,G,H分别是矩形四条边的中点,分别以HF,EG所在的直线为x轴,y轴建立平面直角坐标系,已知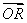 =λ
=λ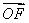 ,
,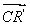 =λ
=λ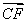 ,其中0<λ<1.
,其中0<λ<1.
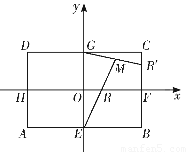
(1)求证:直线ER与GR′的交点M在椭圆Γ: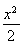 +y2=1上;
+y2=1上;
(2)若点N是直线l:y=x+2上且不在坐标轴上的任意一点,F1、F2分别为椭圆Γ的左、右焦点,直线NF1和NF2与椭圆Γ的交点分别为P、Q和S、T.是否存在点N,使得直线OP、OQ、OS、OT的斜率kOP、kOQ、kOS、kOT满足kOP+kOQ+kOS+kOT=0?若存在,求出点N的坐标;若不存在,请说明理由.
如图,矩形ABCD中,|AB|=2 ,|BC|=2.E,F,G,H分别是矩形四条边的中点,分别以HF,EG所在的直线为x轴,y轴建立平面直角坐标系,已知
,|BC|=2.E,F,G,H分别是矩形四条边的中点,分别以HF,EG所在的直线为x轴,y轴建立平面直角坐标系,已知 =λ
=λ ,
, =λ
=λ ,其中0<λ<1.
,其中0<λ<1.
(1)求证:直线ER与GR′的交点M在椭圆Γ: +y2=1上;
+y2=1上;
(2)若点N是直线l:y=x+2上且不在坐标轴上的任意一点,F1、F2分别为椭圆Γ的左、右焦点,直线NF1和NF2与椭圆Γ的交点分别为P、Q和S、T.是否存在点N,使得直线OP、OQ、OS、OT的斜率kOP、kOQ、kOS、kOT满足kOP+kOQ+kOS+kOT=0?若存在,求出点N的坐标;若不存在,请说明理由.
 ,|BC|=2.E,F,G,H分别是矩形四条边的中点,分别以HF,EG所在的直线为x轴,y轴建立平面直角坐标系,已知
,|BC|=2.E,F,G,H分别是矩形四条边的中点,分别以HF,EG所在的直线为x轴,y轴建立平面直角坐标系,已知 =λ
=λ ,
, =λ
=λ ,其中0<λ<1.
,其中0<λ<1.
 +y2=1上;
+y2=1上;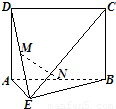
如图,矩形BCC1B1所在平面垂直于三角形ABC所在平面,BB1=CC1=AC=2,![]() ,又E、F分别是C1A和C1B的中点.
,又E、F分别是C1A和C1B的中点.
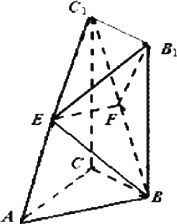
(1)求证:EF∥平面ABC;
(2)求证:平面EFC1⊥平面C1CBB1;
(3)求异面直线AB与EB1所成的角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com