练习册

  • 练习册
  • 试题
    计算焦点弦长可利用上面的焦半径公式. 一般地.若斜率为k的直线被圆锥曲线所截得的弦为AB. A.B两点分别为A(x1.y1).B(x2,y2).则弦长 ,这里体现了解析几何“设而不求 的解题思想, 【查看更多】

     

    题目列表(包括答案和解析)

    有20种不同的零食，它们的热量含量如下：

    110　120　123　165　432　190　174　235　428　318

    249　280　162　146　210　120　123　120　150　140

    (1)以上述20个数据组成总体，求总体平均数与总体标准差．

    (2)设计恰当的随机抽样方法，从总体中抽取一个容量为7的样本，求样本的平均数与标准差．

    (3)利用上面的抽样方法，再抽取容量为7的样本，计算样本的平均数和标准差．这个样本的平均数与标准差和(2)中的结果一样吗？为什么？

    (4)利用(2)中的随机抽样方法，分别从总体中抽取一个容量为10、13、16、19的样本，求样本的平均数与标准差．分析样本容量与样本平均数和样本标准差对总体的估计效果之间有什么关系．

    查看答案和解析>>

    有20种不同的零食，它们的热量含量如下：

    110

    120

    123

    165

    432

    190

    174

    235

    428

    318

    249

    280

    162

    146

    210

    120

    123

    120

    150

    140

    (1)以上述20个数据组成总体，求总体平均数与总体标准差．

    (2)设计恰当的随机抽样方法，从总体中抽取一个容量为7的样本，求样本的平均数与标准差．

    (3)利用上面的抽样方法，再抽取容量为7的样本，计算样本的平均数和标准差．这个样本的平均数与标准差和(2)中的结果一样吗?为什么?

    (4)利用(2)中的随机抽样方法，分别从总体中抽取一个容量为10，13，16，19的样本，求样本的平均数与标准差．分析样本容量与样本平均数和样本标准差对总体的估计效果之间有什么关系．

    查看答案和解析>>

    阅读不等式2x+1＞3x的解法：
    设f(x)=(
    2
    3
    )x+(
    1
    3
    )x    ，函数y=(
    2
    3
    )x    和y=(
    1
    3
    )x    在R内都单调递减；则f（x）在（-∞，+∞）内单调递减．
    ∵f（1）=1，∴当x＜1时，(
    2
    3
    )x+(
    1
    3
    )x＞1，当x≥1时，(
    2
    3
    )x+(
    1
    3
    )x≤1    ．
    ∵3x＞0，∴不等式2^+1＞3x的解为x＜1；
    （1）试利用上面的方法解不等式2x+3x≥5x；
    （2）证明：3x+4x=5x有且仅有一个实数解x=2．

    查看答案和解析>>

    已知数列{an}的第1项是1，第2项是2，以后各项由an=an-1+an-2（n＞2）给出．
    （1）写出这个数列的前5项；
    （2）利用上面的数列{an}，通过公式bn=
    an+1an
    构造一个新的数列{bn}，试写出数列{bn}的前5项．

    查看答案和解析>>

    国家教育部、体育总局和共青团中央曾共同号召，在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动.为此某网站于2010年1月18日至24日，在全国范围内进行了持续一周的在线调查，随机抽取其中200名大中小学生的调查情况，就每天的睡眠时间分组整理如下表所示：

    序号()

    每天睡眠时间

    （小时）

    组中值()

    频数

    频率

    ()

    1

    [4，5)

    4.5

    8

    0.04

    2

    [5，6)

    5.5

    52

    0.26

    3

    [6，7)

    6.5

    60

    0.30

    4

    [7，8)

    7.5

    56

    0.28

    5

    [8，9)

    8.5

    20

    0.10

    6

    [9，10)

    9.5

    4

    0.02

     


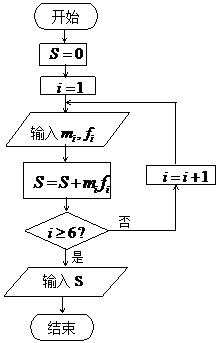    （Ⅰ）估计每天睡眠时间小于8小时的学生所占的百分比约是多少；

    （Ⅱ）该网站利用上面的算法流程图，对样本数据作进一步统计

    分析，求输出的S的值，并说明S的统计意义.

    查看答案和解析>>


    同步练习册答案