题目列表(包括答案和解析)
R)，使得f(x)≥kx十b且g(x)≤kx＋b对一切x>0恒成立？若存在，求出该一次函数的表达式；若不存在，请说明理由．已知函数f(x)=x2，g(x)＝2elnx(x>0)(e为自然对数的底数）．
（1)求F(x)=f(x)－g(x)(x>0)的单调区间及最小值；
（2)是否存在一次函数y=kx+b(k，b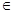
R)，使得f(x)≥kx十b且g(x)≤kx＋b对一切x>0恒成立？若存在，求出该一次函数的表达式；若不存在，请说明理由．
是f(x)的导数.设a1＝1，an+1=an-
(n=1,2,…).(1)求α、β的值；
(2)证明：任意的正整数n，都有an＞
;
(3)记bn=
(n=1,2,…),求数列{bn}的前n项和Sn.
已知函数f(x)|x2－2ax＋b|(x∈R)．给出下列命题：
①f(x)必是偶函数；②当f(0)＝f(2)时，f(x)的图像必关于直线x＝1对称；③若a2－b≤0，则f(x)在区间[a，＋∞]上是增函数；④f(x)有最大值|a2－b|．⑤f(x)的图像必关于直线x＝a对称；⑥f(x)有最小值0；
其中正确的序号是________．
已知函数f(x)x2－x－1，α，β是方程f(x)＝0的两个根(α＞β)，
(x)是f(x)的导数，设
(n＝1，2，…)．
(1)求α，β的值；
(2)已知对任意的正数n有
(n＝1，2，…)，求数列{bn}的前n项和Sn．
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com