练习册

  • 练习册
  • 试题
    5．方程|x|(x-1)-k＝0有三个不相等的实根.则 k的取值范围是 ( ) A. B. C. D. 解析 本题研究方程根的个数问题.此类问题首选的方法是图 象法即构造函数利用函数图象解题.其次是直接求出所有的根． 本题显然考虑第一种方法．如图.作出函数y=|x|·(x-1)的图象. 由图象知当k∈时.函数y=k与y=|x|(x-1)有3个不同的交点. 即方程有3个实根． 答案 A 【查看更多】

     

    题目列表(包括答案和解析)

    设函数f(x)＝－x(x－a)2

    (Ⅰ)当a＝1时，求曲线y＝f(x)在点(2，f(2))处的切线方程；

    (Ⅱ)若a＞0，且方程f(x)＋a＝0有三个不同的实数解，求a的取值范围．

    查看答案和解析>>

    设a为一非零实数，则方程x3＋x2－x＋a＝0

    ①有三个负根；②有两个负根和一个正根；③有一个负根和两个正根；④有三个正根；⑤仅有一个实根，

    以上情形可能成立的有________．

    查看答案和解析>>

    已知函数，若方程f(x)－a＝0有三个不同的实数根，则实数a的取值范围为

    [　　]

    A．(1，3)

    B．(0，3)

    C．(0，2)

    D．(0，1)

    查看答案和解析>>

    已知f(x)＝x2＋bx＋c为偶函数，曲线y＝f(x)过点(2，5)，且g(x)＝(x＋a)f(x)．

    (Ⅰ)若曲线y＝g(x)有斜率为0的切线，求实数a的取值范围

    (Ⅱ)若当x＝－1时函数y＝g(x)取得极大值，且方程g(x)＋b＝0有三个不同的实数解，求实数b的取值范围．

    查看答案和解析>>

    (理科)设定义域为R的函数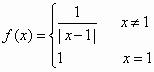，若关于x的方程f2(x)＋bf(x)＋c＝0有三个不同的实数解x1、x2、x3，则等于

    [　　]

    A．5

    B．

    C．13

    D．

    查看答案和解析>>


    同步练习册答案