
题目列表(包括答案和解析)
在△ABC中,M、N分别是AB、AC上的点,![]() =
=![]() =
=![]() .沿MN把△AMN到△
.沿MN把△AMN到△![]() MN的位置,二面角
MN的位置,二面角![]() -MN-B为60°,求证:平面
-MN-B为60°,求证:平面![]() MN⊥平面
MN⊥平面![]() BC.
BC.
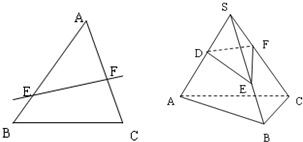 在△ABC中,E、F分别为AB、AC上的点,若
在△ABC中,E、F分别为AB、AC上的点,若| AE |
| AB |
| AF |
| AC |
| S△AEF |
| S△ABC |
| SD |
| DA |
| SE |
| EB |
| SF |
| FC |
| VS-DEF |
| VS-ABC |
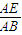 =m,
=m,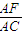 =n,则
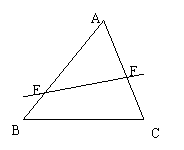
=n,则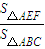 =mn.拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若
=mn.拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若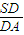 =m,
=m,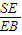 =n,
=n, =p,则
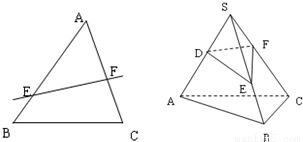
=p,则 = .
= .
在△ABC中,E、F分别为AB、AC上的点,若![]() =m,
=m,![]() =n,则
=n,则
![]() = mn. 拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若
= mn. 拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若![]() = m,
= m,![]() =n,
=n,![]() = p,则
= p,则![]() =
=

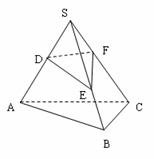
在△ABC中,E、F分别为AB、AC上的点,若![]() =m,
=m,![]() =n,
=n,
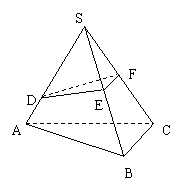 则
则![]() = mn.拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若
= mn.拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若![]() = m,
= m,![]() =
=![]() = n,则
= n,则![]() = .
= .
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com