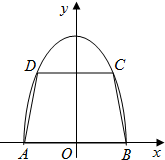如图，有一块半椭圆形钢板，其长半轴长为2r，短半轴长为r，计划将此钢板切割成等腰梯形的形状，下底AB是半椭圆的短轴，上底CD的端点在椭圆上，记CD=2x，梯形面积为S．以AB为x轴，AB中点为原点建立平面直角坐标系．
（Ⅰ）写出该半椭圆的方程；求面积S以x为自变量的函数式，并写出其定义域；
（Ⅱ）设f（x）=S²，求f（x）的最大值，并求出此时的x值（均用r表示）

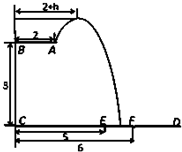某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段，已知跳水板AB长为2m，跳水板距水面CD的高BC为3m，CE=5m，CF=6m，为安全和空中姿态优美，训练时跳水曲线应在离起跳点hm（h≥1）到达距水面最大高度4m，规定：以CD为横轴，CB为纵轴建立坐标系．
（1）当h=1时，求跳水曲线所在的抛物线方程；
（2）若跳水运动员在区域EF内如水时才能达到压水花的训练要求，求达到压水花的训练要求时h的取值范围．

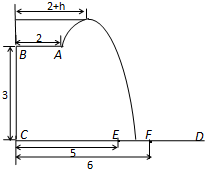某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段．已知跳水板AB长为2m，跳水板距水面CD的高BC为3m．为安全和空中姿态优美，训练时跳水曲线应在离起跳点A处水平距hm（h≥1）时达到距水面最大高度4m．规定：以CD为横轴，BC为纵轴建立直角坐标系．
（1）当h=1时，求跳水曲线所在的抛物线方程；
（2）若跳水运动员在区域EF内入水时才能达到比较好的训练效果，求此时h的取值范围．

研究“刹车距离”对于安全行车及分析交通事故责任都有一定的作用，所谓“刹车距离”就是指行驶中的汽车，从刹车开始到停止，由于惯性的作用而又继续向前滑行的一段距离．为了测定某种型号汽车的刹车性能（车速不超过140km/h），对这种汽车进行测试，测得的数据如表：

刹车时的车速（km/h）	0	10	20	30	40	50	60
刹车距离（m）	0	0.3	1.0	2.1	3.6	5.5	7.8

（1）以车速为x轴，以刹车距离为y轴，在给定坐标系中画出这些数据的散点图；
（2）观察散点图，估计函数的类型，并确定一个满足这些数据的函数表达式；
（3）该型号汽车在国道上发生了一次交通事故，现场测得刹车距离为46.5m，请推测刹车时的速度为多少？请问在事故发生时，汽车是超速行驶还是正常行驶？