
题目列表(包括答案和解析)
.设函数![]() R.
R.
(I)求函数![]() 的最值;
的最值;
(II)给出定理:如果函数![]() 在区间[
在区间[![]() ]上连续,并且有
]上连续,并且有![]() ,那么,函数
,那么,函数![]() 在区间
在区间![]() 内有零点,即存在
内有零点,即存在![]() .
.
运用上述定理判断,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 内是否存在零点.
内是否存在零点.
.设函数![]() R.
R.
(I)求函数![]() 的最值;
的最值;
(II)给出定理:如果函数![]() 在区间[
在区间[![]() ]上连续,并且有
]上连续,并且有![]() ,那么,函数
,那么,函数![]() 在区间
在区间![]() 内有零点,即存在
内有零点,即存在![]() .
.
运用上述定理判断,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 内是否存在零点.
内是否存在零点.
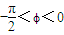 )的最小正周期为π,
)的最小正周期为π,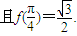
 的取值范围.
的取值范围.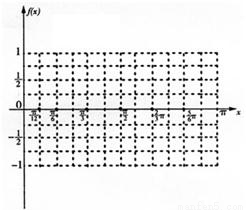
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com