
题目列表(包括答案和解析)
 如图在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点;PA=kAB(k>0),且二面角E-BD-C的平面角大于30°,则k的取值范围是( )
如图在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点;PA=kAB(k>0),且二面角E-BD-C的平面角大于30°,则k的取值范围是( )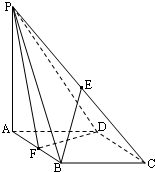 (2010•武清区一模)如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
(2010•武清区一模)如图在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点. (2013•天津模拟)如图在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
(2013•天津模拟)如图在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
| ||
| 2 |
 如图在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,垂足为点A,PA=AB=1,点M,N分别是PD,PB的中点.
如图在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,垂足为点A,PA=AB=1,点M,N分别是PD,PB的中点.| PF |
| FC |
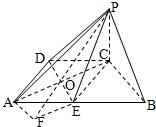 如图在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=
如图在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ADC=| π |
| 2 |
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com