10、如图，PA⊥⊙O所在的平面，AB是⊙O的直径，C是⊙O上的一点，AE⊥PB于E，AF⊥PC于F，给出下列结论：①BC⊥面PAC；②AF⊥面PCB；③EF⊥PB；④AE⊥面PBC．其中正确命题的个数是（　　）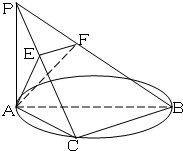

如图：PA⊥⊙O所在的平面，AB是⊙O的直径，C是⊙O上的一点，AE⊥PC，AF⊥PB，给出下列结论①AE⊥BC，②AE⊥PB，③AF⊥BC，④AE⊥平面PBC，其中正确命题的序号是（　　）

如图，PA、PB是⊙O的切线，切点分别为A、B，点C在⊙O上．如果∠P=50°，那么∠ACB等于（　　）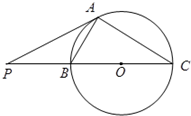

（2012•房山区一模）如图，PA是圆O的切线，切点为A，PO交圆O于B，C两点，PA=

3

，PB=1，则∠ABC=（　　）

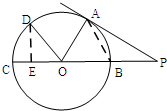如图，PA切圆O于点A，割线PBC经过圆心O，OB=PB=1，OA绕点O逆时针旋转60⁰到OD，则PD的长为（　　）